SUMMARY
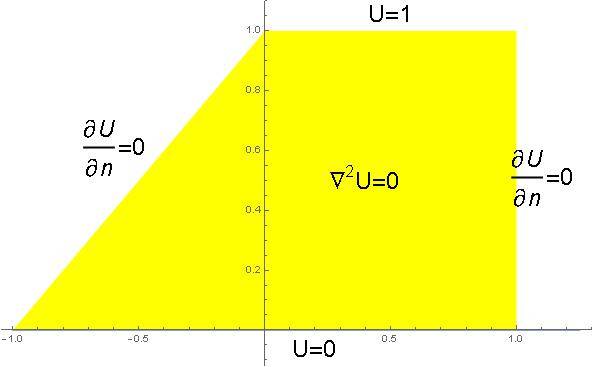
The discussion focuses on solving the Laplace equation on a trapezoid, specifically using analytical methods. The solution presented is u(x,y) = {y, 0 ≤ x ≤ 1, 0 ≤ y ≤ 1; (x + 1)y, -1 ≤ x < 0, 0 ≤ y ≤ 1 + x}. The continuity conditions at x = 0 are analyzed, revealing that while continuity of the function u is achievable, continuity of its derivative cannot be maintained simultaneously. Additionally, the possibility of switching between Neumann and Dirichlet boundary conditions is raised, questioning the existence of an analytical solution under these conditions.
PREREQUISITES
- Understanding of Laplace's equation
- Familiarity with boundary conditions (Neumann and Dirichlet)
- Knowledge of polar and Cartesian coordinates
- Basic concepts of continuity in mathematical functions
NEXT STEPS
- Research analytical methods for solving Laplace's equation in non-rectangular domains
- Explore the implications of Neumann vs. Dirichlet boundary conditions on solutions
- Study the use of continuity conditions in partial differential equations
- Learn about numerical methods for approximating solutions to Laplace's equation
USEFUL FOR
Mathematicians, physicists, and engineers involved in solving partial differential equations, particularly those interested in boundary value problems and analytical methods for complex geometries.