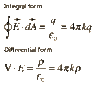Homework Help Overview
The discussion revolves around applying Gauss' Law to determine the electric field generated by a uniformly charged long, thin wire. The original poster seeks guidance on how to approach the problem, specifically using a cylindrical Gaussian surface to analyze the electric field at a radial distance from the wire.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning
Approaches and Questions Raised
- Participants discuss the use of a cylindrical Gaussian surface and the implications of cylindrical symmetry on the electric field's direction. Some participants attempt to derive the electric field expression, while others question the correctness of their calculations and reasoning.
Discussion Status
Several participants have provided insights into the setup of the problem and the application of Gauss' Law. There is a mix of attempts to derive the electric field, with some expressing uncertainty about their calculations. Guidance has been offered regarding the symmetry of the problem and the direction of the electric field.
Contextual Notes
Participants are working under the constraints of a homework assignment, which may limit the information they can share or the methods they can use. There is a focus on ensuring the reasoning aligns with the principles of Gauss' Law and the specific charge distribution described.