bonfire09
- 247
- 0
Homework Statement
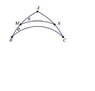
Prove in hyperbolic geometry: In the accompanying figure M and N are the respective (hyperbolic) midpoints of AB and AC and θ and ∅ are the indicated angle measures. Determine, with proof, which of the following is true:
(1): θ=∅ (2): θ<∅ (3): θ>∅ ( stands for phi)
Homework Equations
I have attached a picture of the figure too. Since I am in hyperbolic geometry I get to assume that the internal angle sum of a triangle <180 degrees and AAA congruence for triangles.
The Attempt at a Solution
I don't know where to get started. It looks simple but I am thinking that I need to get congruent triangles in there somehow but I don't know how to. If you can give me a hint that be great.