oxon88
- 176
- 1
Homework Statement
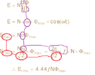
A single phase transformer has the following rating: 120 kVA, 2000 V/100 V, 60 Hz with 1000 primary turns.
Determine:
a) the secondary turns
b) the rated primary and secondary currents
c) the maximum flux
d) given a maximum flux density of 0.25 T, the cross sectional area of the core.
Homework Equations
V2/V1 = N2/N1