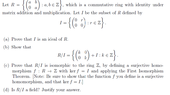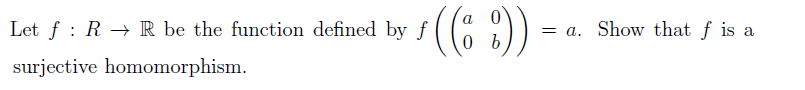SUMMARY
The discussion focuses on the verification of solutions for parts (a), (b), and (c) of a mathematical problem involving ring homomorphisms. The correct approach for part (c) is to define a map \( f: R \to \mathbb{Z} \) given by \( f(A) = A_{12} \) or \( f(A) = A_{11} \), where \( A_{ij} \) denotes the entry in the \( i \)-th row and \( j \)-th column of matrix \( A \). The participants confirm that \( f \) must be a surjective ring homomorphism with kernel \( I \), and they clarify that \( R/I \) is not a field due to the properties of integers.
PREREQUISITES
- Understanding of ring theory, specifically ring homomorphisms
- Familiarity with the first isomorphism theorem for rings
- Knowledge of matrix representation and operations
- Basic concepts of fields and cosets in algebra
NEXT STEPS
- Study the first isomorphism theorem for rings in detail
- Learn about surjective functions and their properties in algebra
- Explore the structure of cosets and their implications in ring theory
- Investigate examples of ring homomorphisms and their kernels
USEFUL FOR
Mathematicians, students studying abstract algebra, and anyone interested in understanding ring homomorphisms and their applications in algebraic structures.