Ideas for a catapult design for an engineering report

[Buggsy GC]

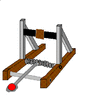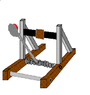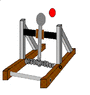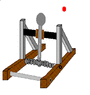
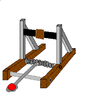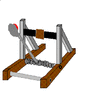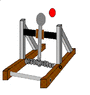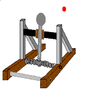
Afternoon every one. I am a first year engineering student in NZ, For my midterm break report I have to design and make a catapult that can meet these specifications.
- hit one target within a 0.1 m radius of a target that is 1 m away horizontally from the base of the model catapult.
- hit one target within a 0.2 m radius of a target that is 2 m away horizontally from the base of the model catapult.
- was built with no more than 20$ NZ.
- there is no restriction on the weigh or size of the projectile or catapult
- the catapult doesn't need to be a traditional catapult, you just have to be able to tabulate the effect of different launch angles OR! initial launch velocity on the horizontal displacement of the projectiles.
If anyone can recommend any books or website to look at for my design, that would be appreciated. The report is due in 24 days so I would like to have a working prototype by 14 days (8/04/2017) from now, at the lattest.
Your's sincerely Buggsy

 

[anorlunda]

Sounds like fun. Do the rules say that the projectile must be solid? With a liquid or gaseous "projectile" you could "hit" everything within the whole range.

Sero=iously, the win may go to the team best able to find a loophole in the rules. Can you post the entire rule set?

 

[Buggsy GC]

Sounds like fun. Do the rules say that the projectile must be solid? With a liquid or gaseous "projectile" you could "hit" everything within the whole range.

Sero=iously, the win may go to the team best able to find a loophole in the rules. Can you post the entire rule set?

here the exact objective from the assignment:
Objective:
To design, build and test a model catapult that can hit the set targets. The experimental results
are to be compared with the theory.
(Note: this image is for reference only. Your model catapult can be of any design or shape.)
Physics involved: Physics of catapults; projectile motion; energy conservation

Tasks to complete (see Figure. 1):
 hit one target within a 0.1 m radius of a target that is 1 m away horizontally from the
base of the model catapult.
 hit one target within a 0.2 m radius of a target that is 2 m away horizontally from the
base of the model catapult.
 You need to predict and plot the theoretical trajectory based on the parameters of
your own model catapult using Excel and include the figure in your report (Section 8
- Results and Discussion). You may make any assumptions if needed, but they must be
clearly stated in your report.
 You will also need to use Excel to tabulate the effect of launch angle OR initial (launch)
velocity on horizontal displacement.

Figure 1: A model catapult that launches a payload to hit a set target.
2017 ENGR101 Assignment 3 Briefing Sheet 3

In your report, you need to provide a list of materials used for building your model and their costs.
The total material cost of your model must not exceed NZD 20 (Recycled materials from your yellow
bin are considered free). You MUST NOT purchase a commercially available catapult model.
Although your main objective is to design, build and test your catapult model, you will need to carry
out rational; quantitative (with numerical results) tests first. You should carry out tests to determine
how far the payload can potentially hit based on the parameters include, but not limited to, the height
of the payload above the base of the catapult, the level of the catapult relative to that of the target,
the weight/size/shape of the payload, the form of energy added into the system etc. Then you should
test your proposed design, quantitatively if at all possible.

The engineering process taught in the lectures and the workshops may be useful when you consider
the problem and work towards your final design. You should use any experience gained to show at
least some degree of improvement in your design during the project.

If you are in doubt about any aspect of this project, use your engineering judgement to make minor
modifications to this specification and include these modifications in your report. Please do NOT email
course tutors or lecturers to see if your proposed modifications or innovations are acceptable.

 

[anorlunda]

Cool. It really does sound like fun.

So, a liquid projectile, or one made of small pellets, would make it easier to hit the target, but would make the calculation and plot requirements more difficult. May I suggest a balloon filled with water or paint as the projectile. Just be very very sure that the balloon bursts when it hits the floor rather than bounce.

You can find many images of catapults on wikipedia, google images, and youtube. Keep in mind perhaps the most important of all engineering principles that is not taught in the books, the KISS principle. Your catapult is nor required to have a long life, nor be mobile, nor to throw heavy projectiles or the longest distances. The simplest catapult that meets the written requirements should be your goal. Simplicity also makes the calculation requirements easier to meet. There is no requirement for size, but too small makes it hard to throw 2m and too big makes it hard to throw such a short distance.

It is also important that your catapult not break during testing. On the other hand, you should avoid the need to calculate strength of materials that would add greatly to the calculation burden. Therefore, size and generous safety margins on strength are among your most important design choices. That would be a good thing to put in your report, "all elements have a minimum 3:1 safety margin on strength", then state how you verified that.

I recommend that you use pictures to inspire your design rather than written or video descriptions of catapult design. The reason is that almost all existing designs are made to meet requirements or goals that you do not share, and thus would be anti-KISS.

Your team should hold a KISS review of any proposed design before building a prototype (you must overcome the predictable urges of nearly everyone to build something cool rather than KISS)

It makes me wish that I could be there as part of your team.

Please to post pictures of your catapult and your results on PF. We'll look forward to hearing about it.

 

[256bits]

 You need to predict and plot the theoretical trajectory based on the parameters of
your own model catapult using Excel and include the figure in your report (Section 8
- Results and Discussion). You may make any assumptions if needed, but they must be
clearly stated in your report.
 You will also need to use Excel to tabulate the effect of launch angle OR initial (launch)
velocity on horizontal displacement.

I would think that is where you would make a start - possible paths of a projectile from catapult to target.
And then make a design on paper to satisfy a chosen launch angle and initial velocity for a chosen projectile to hit the target.
And be prepared to make a lot of scratches and pictures on paper on what is possible.
Put your ideas in the open and trash them out.
If you have to go back to start a few times that is not a setback, but rather optimization towards the goal.

 

[Buggsy GC]

This is a solo project, and right know I am considering using a trebuchet design I found in a book and reducing its size and sling height so it fits the 20$ specification. I'm counting on the law of conservation of energy ( E= dKE+dPE )projectile, to allow me to calculate the final velocity and distance from the KE. Are there any issue I should be wary of with reducing the scale of my engine by 3/4 of its original design.

 

[Ion Aguirre]

Hi
The calculation of a trebuchet is not simple. Its composed by a double pendulum, working as a whip. The rigid arm is the only one which swinging angle is limited by design, while the sling angle isn't. Its not a hard device to be built, but its performance prediction calculation is not trivial.
I'd go for a simple catapult where Energy and hence, motions are easier to be predicted. Most catapults, from Rome to the middle ages, where moved by counterweights or twisted ropes.

 

[Buggsy GC]

Hi
The calculation of a trebuchet is not simple. Its composed by a double pendulum, working as a whip. The rigid arm is the only one which swinging angle is limited by design, while the sling angle isn't. Its not a hard device to be built, but its performance prediction calculation is not trivial.
I'd go for a simple catapult where Energy and hence, motions are easier to be predicted. Most catapults, from Rome to the middle ages, where moved by counterweights or twisted ropes.

is this difficulty in terms of predicting the trajectory of the projectile using different initial velocities because that is the only thing i really need to measure.

 

[Ion Aguirre]

Well, the problem with a Trebuchet, is that double pendulum. The dimensions and weight of both, the rigid arm(the lever) and the sling, are critical in order for the projectile to be shot at the required angle.
It must be noted that, while at a simple catapult, the lever is stopped at a pre-designed point, in a Trebuchet, the sling is able to freely move. The impulse provided by the lever, makes the sling swing, providing more centripetal force. At a given point, and only due to the basket design, the projectile is released. The calculation for that releasing point, intial velocity and shot angle are not easy.
I don't know what's your level in maths, but ... building a mathematical model of a Trebuchet, is not simple.
Weights and lenghts of every part are critical, and hence making predictions requires a good maths modeling and a fine construction.

If it was only a matter of building one, and no predictions were required, that's not so complex. But as you explained at the beggining, predictions are a requirement.

 

[anorlunda]

The trebuchet compared to the catapult is very anti-KISS. So you ignored the advice I have advice is this thread. L

 

[Buggsy GC]

Thank you for the input Ion Aguirre. It sound like you saved be a headache further down the road of this, project.

 

[Buggsy GC]

The trebuchet compared to the catapult is very anti-KISS. So you ignored the advice I have advice is this thread. L

Not intentially I saw the trebuchet and it looked the easiest to build, but I have seen the error of my ways

 

[anorlunda]

Not intentially I saw the trebuchet and it looked the easiest to build, but I have seen the error of my ways

Glad to hear that. Now here's a site with some practical tips. http://www.real-world-physics-problems.com/catapult-physics.html

 

[anorlunda]

Not intentially I saw the trebuchet and it looked the easiest to build, but I have seen the error of my ways

Glad to hear that. Now here's a site with some practical tips using twisted ropes as @Ion Aguirre suggested.
http://www.real-world-physics-problems.com/catapult-physics.html

Next, using the twisted rope design, how would you adjust how far it throws?

 

[anorlunda]

Not intentially I saw the trebuchet and it looked the easiest to build, but I have seen the error of my ways

Glad to hear that. Now here's a site with some practical tips using twisted ropes as @Ion Aguirre suggested.
http://www.real-world-physics-problems.com/catapult-physics.html

Next, using the twisted rope design, how would you adjust how far it throws?

 

[Buggsy GC]

Glad to hear that. Now here's a site with some practical tips using twisted ropes as @Ion Aguirre suggested.
http://www.real-world-physics-problems.com/catapult-physics.html

Next, using the twisted rope design, how would you adjust how far it throws?

View attachment 167554

wouldn't you just adjust the cross bar, as the cross bar is used to control the launch angle of the magonel, or reduce the torque of the twisted rope in the torque bundle

 

[anorlunda]

wouldn't you just adjust the cross bar,

Yup. You need two calibrated positions.

I think you're on your way.

 

[Buggsy GC]

Unlike the Ballista the Mangonel does not release its energy in a linear fashion. The arm makes an arc (part of a circle) with radius equal the arm length. Therefore the Potential Energy is transferred in the Rotational Kinetic Energy. The w stands for the angular velocity and r for the length of the arm. I is the moment of inertial as the arm is a rod and its rotating on its end, I=1/3mr2
U=KErot
U=1/2kx^2=KErot=1/2Iw^2

1/2kx^2=1/2w^2(1/3mr^2)
w=sqrt(2kx^2/mr^2)
The angular velocity is then transferred into linear velocity when the arm comes to an abrupt halt and the missiles continues in the direction of their linear velocity.
does anyone the angular velocity in this example is = to w=sqrt(2kx^2/mr^2) instead of w=sqrt(kx^2/ 1/3mr^2)
retrieved from https://sites.google.com/site/physicsofcatapults/home/how-a-catapult-works-the-physics/mangonel
Also another site shows this equation = √ 3kx^2/mr^2
retrieved from:http://people.cs.ksu.edu/~nhb7817/ScratchCurriculum/Catapult/Physics Calculations for a Mangonel.pdf

 

[Buggsy GC]

Unlike the Ballista the Mangonel does not release its energy in a linear fashion. The arm makes an arc (part of a circle) with radius equal the arm length. Therefore the Potential Energy is transferred in the Rotational Kinetic Energy. The w stands for the angular velocity and r for the length of the arm. I is the moment of inertial as the arm is a rod and its rotating on its end, I=1/3mr2
U=KErot
U=1/2kx^2=KErot=1/2Iw^2
View attachment 196055
1/2kx^2=1/2w^2(1/3mr^2)
w=sqrt(2kx^2/mr^2)
The angular velocity is then transferred into linear velocity when the arm comes to an abrupt halt and the missiles continues in the direction of their linear velocity.
does anyone the angular velocity in this example is = to w=sqrt(2kx^2/mr^2) instead of w=sqrt(kx^2/ 1/3mr^2)
retrieved from https://sites.google.com/site/physicsofcatapults/home/how-a-catapult-works-the-physics/mangonel
Also another site shows this equation = √ 3kx^2/mr^2
retrieved from:http://people.cs.ksu.edu/~nhb7817/ScratchCurriculum/Catapult/Physics Calculations for a Mangonel.pdf

The maths of the second website makes sense to me. so my new question is how do you experimentally calculate the force of the spring since I don't know the spring constant for the rope wheel spring I've made, I'm thinking of just seeing how many rocks it takes to set the catapults arm in firing position and then using weighing those rocks and using Newtons second law to convert the g to Newtons. F=ma, m*-9.81=F

 

[Buggsy GC]

the torsion mangonel is extremely anti kiss

 

[Buggsy GC]

I figured it out I'm sorry it took so long, I went back to some articles and remembered that catapult are really energy inefficient especially my design, and once you factor that energy inefficiency percentage, all the answers made sense, I was consistently off my over a factor of 10. Thank you for all your help especially you anorlunda, I'm sorry that my question were so constant and acted like a baby at time, best wishes buggsy

 

[Anarion]

Sounds like fun. Do the rules say that the projectile must be solid? With a liquid or gaseous "projectile" you could "hit" everything within the whole range.

Sero=iously, the win may go to the team best able to find a loophole in the rules. Can you post the entire rule set?

Hehe. "If you are not cheating, you are not trying hard enough."