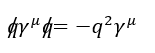SUMMARY
The identity involving four-vectors and Gamma matrices is confirmed to be correct, specifically for a generic four-vector "q". The defining property of the Gamma matrices, given by the anticommutation relation \(\{\gamma^{\mu},\gamma^{\nu}\}=2 \eta^{\mu \nu}\), is essential for the proof. The expression simplifies to \(2q_{\alpha} \gamma^{\alpha} q^{\mu} - q^2 \gamma^{\mu}\) through the application of the Einstein summation convention. Additionally, the discussion touches on the LaTeX package slashed.sty for typesetting Feynman slashes.
PREREQUISITES
- Understanding of Gamma matrices and their properties in quantum field theory
- Familiarity with four-vectors and their notation in physics
- Knowledge of the Einstein summation convention
- Basic proficiency in LaTeX for typesetting mathematical expressions
NEXT STEPS
- Study the properties of Gamma matrices in quantum electrodynamics
- Learn about the implications of the anticommutation relations in particle physics
- Explore the use of the Einstein summation convention in advanced physics problems
- Research LaTeX packages for advanced typesetting, including slashed notation
USEFUL FOR
This discussion is beneficial for theoretical physicists, graduate students in quantum mechanics, and anyone interested in advanced topics related to Gamma matrices and four-vector calculus.