Impulse and Momentum of a crate

[jjiimmyy101]

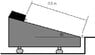
Question (I added a picture): The free-rolling ramp has a mass of 40 kg. A 10 kg crate is released from rest at A and slides down 3.5 m to point B. If the surface of the ramp is smooth, determine the ramp's speed when the crate reaches B. Also, what is the velocity of the crate?

This is what I did for finding the velocity of the ramp:

1) \sigma mv1 = \sigma mv2

2) mass ramp * (velocity ramp)1 + mass crate * (velocity crate)1 = mass ramp * (velocity ramp)2 + mass crate *(velocity crate)2

3) 40*Vr + 0 = 40*Vr2 + 10*Vc2

Too many unknowns?

This is what I did for finding the velocity of the crate:

1) Vc2^2 = Vinitial^2 + 2*a*(S-Sinitial)

= 0 + 2 * 4.905 * 3.5
Vc2 = 5.86 m/s

2) I can substitute this into the first equation, but I still have too many unknowns. What should I do next?

 

[Chen]

The crate is released from rest, therefore its initval velocity Vr is zero.

(Don't forget you can also appy the rules of conservation of energy, even though it's not needed in this case. There are only two kind of forces in the problem - the gravitational force, which is preservative, and the normal force which does no work since it's always perpendicular to the displacement of the objects.)

 

[jjiimmyy101]

Vr is the velocity of the ramp
Vc is the velocity of the crate

 

[Chen]

Both V_R_1 and V_C_1 equal 0 since the system is at rest before it's released.

 

[jjiimmyy101]

The velocity of the crate and the velocity of the ramp are in opposite directions, right?

So the equation is
0 = -40 * Vr2 + 10 * Vb2 and since Vb2 = 5.86 m/s

Vr2 = 1.465 m/s in the opposite direction of the crate. Is it right?

 

[Chen]

I would think so, unless you made a mistake in some of the calculations. The way is correct.

 

[jjiimmyy101]

thank-you