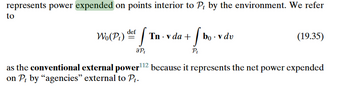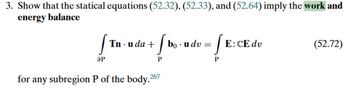Klaus3
- 26
- 3
The definitions of power and work in continuum mechanics are:
$$ W = \int T \cdot u dA + \int b \cdot u dV (1) $$
$$ P = \int T \cdot v dA + \int b \cdot v dV (2) $$
##u## is the displacement vector, ##v## is the velocity, ##T## is the cauchy stress tensor, ##b## is the body force ##A## is area and ##V##, volume. ##W## is work and ##P## is power
I tried to show that ## P = \frac{dW}{dt} ##, but failed
At first i thought integrating Eq (1) but i was intimidated by the amount of algebra necessary to put the derivative inside the integral, then i tried integrating Eq (2)
$$ \int Pdt = \int \int T \cdot v dAdt + \int \int b \cdot v dV dt(3) $$
Commuting the Space and time integrals and applying the definition of velocity
$$ \int Pdt = \int \int T \cdot \frac{du}{dt} dtdA + \int \int b \cdot \frac{du}{dt} dtdV (4) $$
$$ \int Pdt = \int \int T \cdot dudA + \int \int b \cdot dudV (5) $$
And here is where i'm stuck. Equation (5) doesn't seem to match with equation (1) and i don't know if there is any mistake in the derivation. Instead of ##du## it should have been ##u## in Eq (5), but a priori i don't know how to make it appear. Any clues? Thanks
$$ W = \int T \cdot u dA + \int b \cdot u dV (1) $$
$$ P = \int T \cdot v dA + \int b \cdot v dV (2) $$
##u## is the displacement vector, ##v## is the velocity, ##T## is the cauchy stress tensor, ##b## is the body force ##A## is area and ##V##, volume. ##W## is work and ##P## is power
I tried to show that ## P = \frac{dW}{dt} ##, but failed
At first i thought integrating Eq (1) but i was intimidated by the amount of algebra necessary to put the derivative inside the integral, then i tried integrating Eq (2)
$$ \int Pdt = \int \int T \cdot v dAdt + \int \int b \cdot v dV dt(3) $$
Commuting the Space and time integrals and applying the definition of velocity
$$ \int Pdt = \int \int T \cdot \frac{du}{dt} dtdA + \int \int b \cdot \frac{du}{dt} dtdV (4) $$
$$ \int Pdt = \int \int T \cdot dudA + \int \int b \cdot dudV (5) $$
And here is where i'm stuck. Equation (5) doesn't seem to match with equation (1) and i don't know if there is any mistake in the derivation. Instead of ##du## it should have been ##u## in Eq (5), but a priori i don't know how to make it appear. Any clues? Thanks