Increasing Flow rate through system

[_Bd_]

Hi,
I'm building an experimental set-up for some heat exchanger I'm trying to analyze, I want to maximize the flow through this little piece.
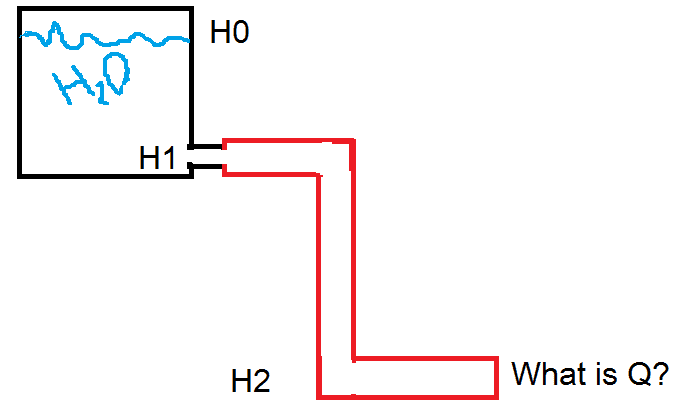
I have a stable temperature bath, (see picture) that has an evacuation valve on the bottom.

I only took introduction to Fluid Dynamics (found it amazing BTW). Anyways, I have a question as I always found this topics to be counter-intuitive and I just wanted to make sure.
If you look at the picture, and assuming some derived equations from Bernoulli's principle:

Volumetric flow rate is constant (right?)

Volumetric flow rate = velocity * Area of pipe

Velocity = Sqrt (2 * g * h)

My question is, on the drawing, the red pipe, does it help increase the flow rate or not?

Here's my line of reasoning:

- I would assume it DOES NOT, as the flow rate is limited by the orifice in which the water enters the piping system, so the max. flow rate I could ever get from this is the difference of H1 and H0 x the diameter of that orifice.

However, if say I took a point at H2 and tried to find out the velocity, in theory using the same equation I should have a higher velocity (differenc between H2 and H0) and therefore a higher flow rate? (this doesn't make sense in my opinion)

I just wanted some clarification on how to apply Bernoulli's principle in this particular case. As mentioned earlier I want to maximize the flow but I don't really know how to without using a submersible pump or something of the sort.NOTE: (There is a pump at the end that brings everything back to the top, so H0 remains constant)

 

[JBA]

You should use h = Ho - H1 in your equation for calculating the flow rate through the orifice because the red pipe will not increase the flow rate. In fact, if insufficiently sized for gravity flow, it can actually restrict the flow rate.

Think of your red pipe in terms of having a basin under the tank orifice attached to the red down pipe from your tank; and, assuming no flowing loss in your red pipe or flow restriction at the bottom of the pipe, then the larger red pipe will be only partly full of the falling liquid (like an enclosed waterfall).

While your volumetric equation is correct, for liquids, it only applies to the smallest flow restriction and is best expressed as mass flow in lbs/hr (kg/hr). The Bernoulli equation would only apply for the red pipe if you were flowing a gas (or flashing liquid) that would expand to accommodate the increased pipe diameter; but, the mass flow applies to both liquid and gases.

For a gas, when the volume flow in cfm increases in the larger red pipe, the density of the gas decreases, so the mass flow of the gas is identical through both the smaller orifice at the top and the larger red pipe below.

If you use a centrifugal pump at the bottom of the pipe, be sure to size your downpipe to insure its minimum flow rate is greater than your pump rated flow rate. If you fail to do so, you may starve the pump inlet and create cavitation in the pump that will damage its impeller.

On another similar project I found the following chart that specifies the minimum vertical pipe diameters for gravity fed water flow without flowing pressure losses that may be of benefit to you.

 

[Perq]

^ This is false.

You still have fluid in the pipe, which does increase the pressure, which can in turn, potentially, increase the fluid flow. You WILL get higher static pressure on the bottom using the H0-H2, because it is contained inside the tube, instead of being depressurized to the environment (as it would be at H1).

(I recall Bernoulli doing this trick-experiment with barrel exploding due to pressure contained in a little pipe, which he held from the top of a building - or something like that)

The flow won't be constant, as H0 will be changing, unless container is big enough to threat it as almost steady (flow is << than the volume of the tank).

The flow would increase, assuming that hydraulic resistance won't be higher than gain of pressure from increased height drop (main thing is the diameter of the tube).

 

[Chestermiller]

With the tube attached, you will get higher flow rate because the pressure at the entrance to the tube will drop below atmospheric. Just call this pressure p_b, and apply Bernoulli to (a) the tank between the upper surface and the oriface and (b) the tube between the oriface and the exit. The deficit in fluid pressure at the entrance to the tube will just be equal to the static head of fluid in the tube (since there is no velocity change in the tube).

Chet

 

[JBA]

With the tube attached, you will get higher flow rate because the pressure at the entrance to the tube will drop below atmospheric. Just call this pressure p_b, and apply Bernoulli to (a) the tank between the upper surface and the oriface and (b) the tube between the oriface and the exit. The deficit in fluid pressure at the entrance to the tube will just be equal to the static head of fluid in the tube (since there is no velocity change in the tube).

Chet

Thank you for the correction to my error. I should have realized the potential of the gravity effect between H1 and H2 to create a lower than atmospheric discharge pressure for the orifice.