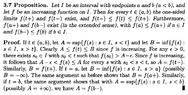Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...
I am currently reading Chapter 3: Continuous Functions on Intervals and am currently focused on Section 3.1 Limits and Continuity ... ...
I need some help in understanding the proof of Proposition 3.14 ...Proposition 3.14 and its proof read as follows:
View attachment 9536
In the above proof by Browder we read the following:
" ... ... For any $$d \in I, d$$ not an endpoint of $$I$$ we know (Proposition 3.7) that $$f(d-)$$ and $$f(d+)$$ exist with $$f(d-) \leq f(d) \leq f(d+)$$, so $$d \in D$$ if and only if $$f(d-) \lt f(d+)$$. ... ... "My question is as follows:
Can someone please demonstrate (rigorously) exactly why/how it follows that $$d \in D$$ if and only if $$f(d-) \lt f(d+)$$. ... ... Help will be much appreciated ...
Peter
=======================================================================================The above post mentions Browder Proposition 3.7 ... so I am providing the text of that proposition ... as follows:
View attachment 9537
Hope that helps ...
Peter
I am currently reading Chapter 3: Continuous Functions on Intervals and am currently focused on Section 3.1 Limits and Continuity ... ...
I need some help in understanding the proof of Proposition 3.14 ...Proposition 3.14 and its proof read as follows:
View attachment 9536
In the above proof by Browder we read the following:
" ... ... For any $$d \in I, d$$ not an endpoint of $$I$$ we know (Proposition 3.7) that $$f(d-)$$ and $$f(d+)$$ exist with $$f(d-) \leq f(d) \leq f(d+)$$, so $$d \in D$$ if and only if $$f(d-) \lt f(d+)$$. ... ... "My question is as follows:
Can someone please demonstrate (rigorously) exactly why/how it follows that $$d \in D$$ if and only if $$f(d-) \lt f(d+)$$. ... ... Help will be much appreciated ...
Peter
=======================================================================================The above post mentions Browder Proposition 3.7 ... so I am providing the text of that proposition ... as follows:
View attachment 9537
Hope that helps ...
Peter
Attachments
Last edited: