Index of refraction when total internal reflection ceases

[floridianfisher]

light refractions problem

I don't even know where to start with this problem. Can someone please help me out?
As shown in Figure P22.49, a light ray is incident normal to on one face of a 30°-60°-90° block of zircon(n= 1.923) that is immersed in water.

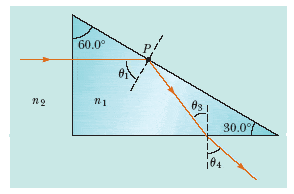
Figure P22.49
(a) Determine the exit angle 4 of the ray.
4 = wrong check mark°
(b) A substance is dissolved in the water to increase the index of refraction. At what value of n2 does total internal reflection cease at point P?
n2 =

 

[bel]

For (a) : The light beam obviously entered at a normal to the shortest side of the triangular block since there wasn't any refraction, so using the fact that a triangle in a plane has a sum of internal angles of one hundred and eighty degrees, $$\theta_1=60^\circ$$. And I suppose you know that in one single medium, for a reflection, incident angle equals reflected angle, using this, and Snell's law and the sum of internal angles for a triangle, you should be able to figure this out. Hope this helped.

For (b) : Total internal reflection occurs if critical angle is smaller than incident angle. Using Snell's law, the critical angle is the arcsine of $$\frac{n_2}{n_1}$$.

 

[floridianfisher]

so using the sum of internal angles it looks like theta 3 would be 30 degrees? Because if you split the reflected ray there is a 30-60-90 triangle?

 

[floridianfisher]

Homework Statement

As shown in Figure P22.49, a light ray is incident normal to on one face of a 30°-60°-90° block of zircon that is immersed in water.

(b) A substance is dissolved in the water to increase the index of refraction. At what value of n2 does total internal reflection cease at point P?

Homework Equations

theta critical= arcsin(n2/n1) and total internal reflection ceases when theta critical is less than theta incident

The Attempt at a Solution

theta 4 is 46.16. I used 59.9=arcsin(n2/1.333) and got n2=1.15 but that's not correct but i don't understand because that is when theta critical is less than theta incident. theta incident is 60

 

[andrevdh]

You need to consider total internal reflection at point P (at $$\theta _1$$).

Also n1 is for zirconium.