Discussion Overview
The discussion focuses on the estimation of magnetising losses in an induction motor under no-load conditions. Participants explore the relationships between various electrical parameters, including power factor, resistance, and reactance, while addressing the implications of these calculations on the understanding of core losses in the motor.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
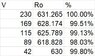
- One participant presents calculations for the magnetising resistance (R0) and reactance (X0) based on given voltage, current, and power factor, questioning the large magnetisation losses compared to actual stator power.
- Another participant challenges the use of the coefficient 1.732 in the power factor calculation, seeking clarification on its origin and the definition of power factor.
- Some participants suggest that the exercise should consider stator power as magnetic losses alongside windage and friction, noting that these losses are constant when speed is constant.
- There is a discussion about the relationship between magnetic losses and voltage, with one participant asserting that if voltage is zero, only windage and friction losses remain.
- One participant expresses confusion over how windage and friction losses were derived from a plotted curve, indicating a need for clarification on the methodology used.
- Another participant calculates windage and friction losses and discusses the implications for R0, while also questioning the rationale behind the formula involving voltage squared and the factor of 3 in relation to X0.
- Clarification is sought regarding the term "line voltage," with a participant explaining the differences between phase-to-neutral and phase-to-phase voltages in the context of three-phase systems.
Areas of Agreement / Disagreement
Participants express differing views on the calculations and interpretations of power factor, magnetising losses, and the definitions of voltage in three-phase systems. There is no consensus on the correct approach to estimating magnetising losses or the implications of the calculations presented.
Contextual Notes
Participants note potential limitations in their calculations, including assumptions about the nature of the power factor, the definitions of voltage in different configurations, and the dependency of losses on voltage levels. Some calculations may rely on specific interpretations of the system's parameters.