L = K - U
- 4
- 1
I could've peeked at the solution manual and end with it at that. However, I'm trying to change this nasty habit and solve this problem myself. I might be too ambitious. Here goes.
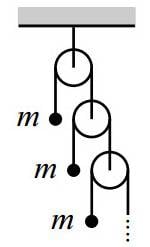
Consider the infinite Atwood's machine shown. A string passes over each pulley, with one end attached to a mass and the other end attached to another pulley. All the masses are equal to m, and all the pulleys and strings are massless. The masses are held fixed and then simultaneously released. What is the acceleration of the top mass? (You may define this infinite system as follows. Consider it to be made of N pulleys, with a nonzero mass replacing what would have been the (N+1)th pulley. Then take the limit as N \rightarrow \infty)
Newton's Second Law : \sum \mathbf{F} = m\mathbf{a}
Taking the upward direction to be positive, I started with Newton's Second law of motion for the Nth mass
\dfrac{T}{N} - mg = ma_N.
With this equation, I can quickly see that the mass at infinity would have an acceleration downwards of magnitude g and the tension in the string will be zero.
I then tried to reduce the problem to a single atwood machine with mass m on the left and (N - 1)m on the right. Solving using Newton's Laws and 'Conservation of string', I ended with
a = \bigg(1 - \dfrac{2}{N} \bigg)g
taking the limit as N approches infinity, I will get an acceleration upwards with a = g. However, the solution says (I'm only peeking at the answer, I swear.) that the correct answer is a = \dfrac{g}{2}
My last resort is to return to the equation of motion for the Nth mass and try to find the relationship between all of the masses. I used a bunch of 'Conservation of Strings' and ended up with an equation that looks like it should mean something.
a^\prime_N = a_N + \sum_{i = 1}^{N-1} 2^{(N-1) - i}a_i
with a^\prime_N being the acceleration of the Nth mass in the frame accelerating downwards. From here, I tried to take the limit of the sum above but It blows up to infinity.
I'm truly stuck at this one and I need some insight on this problem.
Thanks in advance.
Homework Statement
Consider the infinite Atwood's machine shown. A string passes over each pulley, with one end attached to a mass and the other end attached to another pulley. All the masses are equal to m, and all the pulleys and strings are massless. The masses are held fixed and then simultaneously released. What is the acceleration of the top mass? (You may define this infinite system as follows. Consider it to be made of N pulleys, with a nonzero mass replacing what would have been the (N+1)th pulley. Then take the limit as N \rightarrow \infty)
Homework Equations
Newton's Second Law : \sum \mathbf{F} = m\mathbf{a}
The Attempt at a Solution
Taking the upward direction to be positive, I started with Newton's Second law of motion for the Nth mass
\dfrac{T}{N} - mg = ma_N.
With this equation, I can quickly see that the mass at infinity would have an acceleration downwards of magnitude g and the tension in the string will be zero.
I then tried to reduce the problem to a single atwood machine with mass m on the left and (N - 1)m on the right. Solving using Newton's Laws and 'Conservation of string', I ended with
a = \bigg(1 - \dfrac{2}{N} \bigg)g
taking the limit as N approches infinity, I will get an acceleration upwards with a = g. However, the solution says (I'm only peeking at the answer, I swear.) that the correct answer is a = \dfrac{g}{2}
My last resort is to return to the equation of motion for the Nth mass and try to find the relationship between all of the masses. I used a bunch of 'Conservation of Strings' and ended up with an equation that looks like it should mean something.
a^\prime_N = a_N + \sum_{i = 1}^{N-1} 2^{(N-1) - i}a_i
with a^\prime_N being the acceleration of the Nth mass in the frame accelerating downwards. From here, I tried to take the limit of the sum above but It blows up to infinity.
I'm truly stuck at this one and I need some insight on this problem.
Thanks in advance.