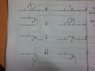Infinitely Long Wire with Loop (Magnetic Field)

[Hitchslaps]

Homework Statement

The wires below are infinitely long and some of them are with loops and semi loops. The current I is constant. What is the magnetic field in point O, when R is the distance from it?

Questions:
In F, E and H, the magnetic field exerted by the terminal infinitely long wire is 0 because it is 180 degrees?
If the loop is a semi-circle, I use B/2? If the loop is a quarter of a circle, then B/4 and so on?

How to solve for G?

Homework Equations

B= μI/2R
B=2μI/4piR

The Attempt at a Solution

I included in my calculations the magnetic fields of both the infinite wire and the loop.

A: μI/2R Outwards
B: μI/2R + 2μI/4piR Outwards
C: μI/2R - 2μI/4piR Outwards
D: μI/2R - μI/2R +2μI/8piR = 2μI/8piR Inwards
E: 2μI/8piR Inwards
F: μI/2R + 2μI/16piR Inwards
G: ?
H: μI/2R + 2μI/8piR + μI/2R Inwards

 

[Simon Bridge]

You are asked to find the field at point O right?
Then yes: EF and H have sections of wire that do not contribute.
If B is the field of a complete loop, then an 1/nth of a loop contributes B/n.

You have equations:
BL = μI/2R <---<<< for the field center of a current loop radius R
BW =2μI/4piR=μI/(2piR) <---<<< the field radial distance R from infinite straight wire

This makes for a nice way to summarize your answers to make double-checking easy:

If we make BW=B, then BL=pi.B

Using + to indicate "into the page"
Your answers are:

A: -B
B: -(pi+1)B (what is the total current at the place the loop and the wire meet?)
C: -(pi-1)B (there is another difference between C and B)
D: +(pi-pi+1/2)B = B/2 (are you saying the two wires cancel out? Check by RH rule.)
E: +B/2 (which is half that due to a wire - does that make sense?)
F: +(pi+1/4)B
G: ?
H: +(pi + 1/2 +pi)

... I think one of us got confused between the contributions of the wire and that of the loop-section.

Checking:
http://hyperphysics.phy-astr.gsu.edu/HBASE/magnetic/curloo.html#c2
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html

$$B_L=\frac{\mu_0 I}{2R}=\pi\frac{\mu_0 I}{2\pi R}=\pi B_W$$

For some of them, only half the wire contributes to the field.
Did you check that the final direction you gave is that for the net field - i.e. a negative magnitude into the page is a positive magnitude out of the page - so the net direction is "outwards".

For G - it's the same as the others: what's the problem?

 

[Hitchslaps]

Thank you for your help!
I confused the two equations, sorry.

My answers now:
A: -B
B: -(pi+1)B The current is NI, which is 2I? So the loop’s magnetic field is μ2I/2R= μI/R.
C: +(+pi-1)B The wires don’t meet, so the current stays the same?
D: +(2+1/2pi)B
E: +pi.B/2
F: +(1/4pi+1)B
G: +(2+1/2pi)B
H: +(1 +1/2pi)Byes, these are all net directions, assuming I'm correct.

 

[Simon Bridge]

It's interesting about the gap in C isn't it?
It may just be that the gap is supposed to be invisibly small and shown large for emphasis.
I think you have the right of it: one subtracts the wire while the other adds it.

Sometimes you have to account for gaps by subtracting the field that would otherwise be present.

You seem to have a handle on what's required enough to check your own math - well done.