- #1
Loopas
- 55
- 0
Homework Statement
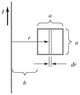
Determine the emf induced in the square loop in the figure if the loop stays at rest and the current in the straight wire is given by I(t)=(15.0A)sin(2500t) where t is in seconds. The distance a is 12.0 cm, and b is 15.0 cm.
Homework Equations
emf = Δmagneticflux/Δt
magnetic flux = BA
magnetic field from infinite wire = (μI)/(2*pi*R)
The Attempt at a Solution
I tried using the using the magnetic field from the wire and the area of the square loop to calculate magnetic flux. My final answer was: (2.9*10^-7*sin(2500t))/t
But this isn't the right answer, so I'm guessing that I have to integrate with Faraday's Law but I am clueless about integrals
 Finally found it!
Finally found it!