- #1
tom8
- 19
- 0
Consider the Lindhard response function:
[tex]\chi(\vec{q})=\int\frac{d\vec{k}}{(2\pi)^d}\frac{f_\vec{k}-f_{\vec{k}+\vec{q}}}{\epsilon_\vec{k}-\epsilon_{\vec{k}+\vec{q}}}[/tex]
where ##\vec{q}## is the wavevector, ##\epsilon## is the free electron energy and ##f## is Fermi-Dirac distribution function. For 1D near ##2k_F##, this reduces to:
[tex]\chi(q)=-e^2n(\epsilon_F)\ln\frac{q+2\vec{k}_F}{q-2\vec{k}_F}[/tex]
where ##n(\epsilon_\vec{F})## is the density of states. Clearly ##\chi(\vec{q})## diverges near ##\vec{q}=2\vec{k}_F##.
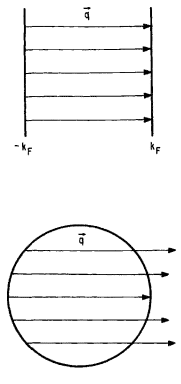
It is argued (see the picture below) that this divergence is due to Fermi surface nesting, which is represented by the arrows in the picture. What I do not understand is that why, in the 2D case, the arrows are restricted to be horizontal? I can still draw an arrow in any direction since this is a Fermi surface and all points have the same energy and are thus identical...
[tex]\chi(\vec{q})=\int\frac{d\vec{k}}{(2\pi)^d}\frac{f_\vec{k}-f_{\vec{k}+\vec{q}}}{\epsilon_\vec{k}-\epsilon_{\vec{k}+\vec{q}}}[/tex]
where ##\vec{q}## is the wavevector, ##\epsilon## is the free electron energy and ##f## is Fermi-Dirac distribution function. For 1D near ##2k_F##, this reduces to:
[tex]\chi(q)=-e^2n(\epsilon_F)\ln\frac{q+2\vec{k}_F}{q-2\vec{k}_F}[/tex]
where ##n(\epsilon_\vec{F})## is the density of states. Clearly ##\chi(\vec{q})## diverges near ##\vec{q}=2\vec{k}_F##.
It is argued (see the picture below) that this divergence is due to Fermi surface nesting, which is represented by the arrows in the picture. What I do not understand is that why, in the 2D case, the arrows are restricted to be horizontal? I can still draw an arrow in any direction since this is a Fermi surface and all points have the same energy and are thus identical...