Instantaneous Particle Velocity from Wave

In summary, the conversation discusses finding the instantaneous velocity of a particle using the equation D(x,t) = Asin(kx-ωt+ϕ). The attempt at a solution involves taking the derivative of displacement and plugging in known values to determine the answer. However, since there is no specified value for time or distance, the conversation suggests using an indirect value at point 1 to determine the phase and ultimately find the velocity.
  • #1
rocapp
95
0

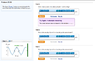
Homework Statement


See the attached picture.



Homework Equations


D(x,t) = Asin(kx-ωt+ϕ)


The Attempt at a Solution


The instantaneous velocity of a particle would be the derivative of displacement:
D'(x,t) = -ωAcos(kx-tω+ϕ)

Then plug in the known values:
= -18.84cos((π/15)x-3πt)

The above should be the answer, but since I do not have a specified value for time or distance, I am not sure how to come to a numerical answer. Thanks in advance!
 

Attachments

  • Screen shot 2013-01-25 at 2.06.12 PM.png
    Screen shot 2013-01-25 at 2.06.12 PM.png
    29.3 KB · Views: 798
Physics news on Phys.org
  • #2
rocapp said:
since I do not have a specified value for time or distance
You have an indirect one: At point 1, the position is 0. This allows to determine a value for the phase (kx-ωt+ϕ), which you can use in the equation for the velocity.
 
  • #3
Thanks!
 

FAQ: Instantaneous Particle Velocity from Wave

1. What is instantaneous particle velocity from wave?

Instantaneous particle velocity from wave refers to the speed at which individual particles in a medium are moving at a specific moment in time as a result of a wave passing through the medium.

2. How is instantaneous particle velocity from wave measured?

Instantaneous particle velocity from wave can be measured using various techniques such as Doppler effect, laser interferometry, or pressure sensors. These techniques allow for the detection and measurement of the small changes in position of individual particles in a wave.

3. What factors affect instantaneous particle velocity from wave?

The instantaneous particle velocity from wave is affected by the properties of the medium, such as density, elasticity, and viscosity. It is also influenced by the characteristics of the wave, such as frequency, amplitude, and wavelength.

4. How does instantaneous particle velocity from wave relate to wave speed?

Instantaneous particle velocity from wave is related to wave speed through the formula v = λf, where v is the wave speed, λ is the wavelength, and f is the frequency. This means that as the wave speed increases, so does the instantaneous particle velocity.

5. Why is instantaneous particle velocity from wave important in scientific research?

Instantaneous particle velocity from wave is an important factor in understanding and modeling various phenomena, such as sound and seismic waves, ocean currents, and electromagnetic waves. It also plays a crucial role in fields such as acoustics, fluid dynamics, and geophysics.

Similar threads

What is the value of ω for the following wave?
Replies
5
Views
918
Calculate Distance Traveled: Instantaneous vs. Average Velocity
Replies
5
Views
1K
Wave equation, wavelenght not given
Replies
6
Views
1K
Standing wave transverse motion and amplitude
Replies
5
Views
2K
Wave movement and particle movement
Replies
23
Views
456
Is D(x,t) = ln(ax+bt) a solution to the wave function?
Replies
9
Views
4K
How Do You Calculate Instantaneous Velocity at a Midpoint in Particle Motion?
Replies
7
Views
2K
Transverse Wave Velocity/Acceleration
Replies
10
Views
5K
Amplitude of Wave at 5pi/6 Radians in Cycle, y = Asin(kx-wt)
Replies
8
Views
2K
Wave function - displacement - transverse wave
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top