maistral
- 235
- 17
Hi. So I'm trying to use Laplace transforms in inverting a particular s-function via the convolution formula.
I ended up with this terrifying-looking thing:
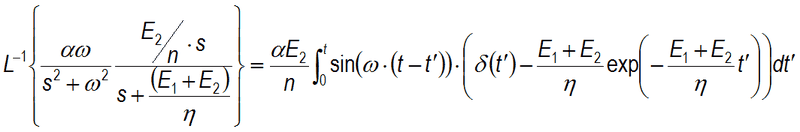
So distributing, I ended up with:
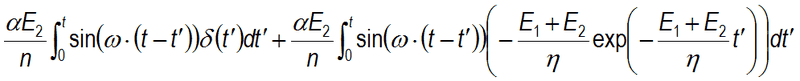
Evaluating the second integral poses no problem for me (although I think the integration will definitely be 'hairy'). I have a problem with the first integral though. How on Earth do I integrate the dirac delta? Help! I am totally at a loss here. Or am I doing something wrong?
I ended up with this terrifying-looking thing:
So distributing, I ended up with:
Evaluating the second integral poses no problem for me (although I think the integration will definitely be 'hairy'). I have a problem with the first integral though. How on Earth do I integrate the dirac delta? Help! I am totally at a loss here. Or am I doing something wrong?