Evaluation of an improper integral leading to a delta function

[chiraganand]

TL;DR Summary

I have included some improper integrals with the solutions and would like help as to the approach needed to reach the solutions

Hi,

I have pasted two improper integrals. The text has evaluated these integrals and come up with answers. I wanted to know how these integrals have been evaluated and what is the process to do so.
Integral 1

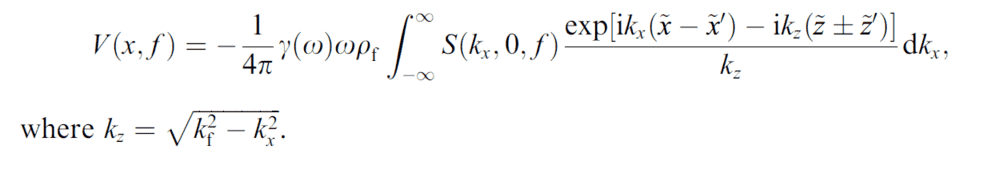
Now the 1st integral is again integrated

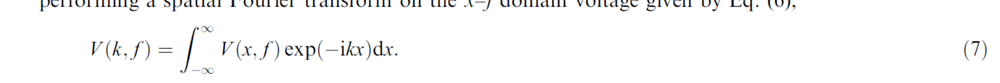
Now the text accompanying the integration

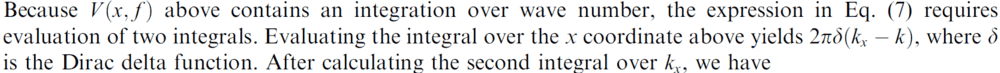
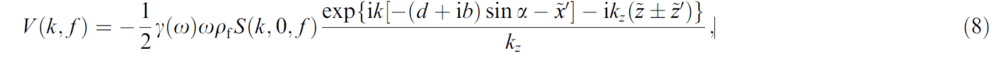
So can some one please help me in figuring out how the integration over x coordinate gives the delta function and how over the kx coordinate gives the equation (8). Links to formulas would be helpful. Any help would be quite appreciated

 

[jasonRF]

You haven't given us enough information to make sense out of (8). What are $d$, $b$ and $\alpha$? Also, your first equation has no $x$ in it at all, only $\tilde{x}$ and $\tilde{x}^\prime$. I don't actually want you to answer these questions, by the way.

To me this looks like the kind of integral you get when are using Fourier analysis to solve PDEs. What you need to understand is the basic idea, then your specific integral will be up to you. Consider
$$
\begin{eqnarray*}
\int_{-\infty}^\infty \int_{-\infty}^\infty \, F(\beta) e^{i (k - \beta)x} d\beta\, dx
& = &
\int_{-\infty}^\infty F(\beta) \left( \int_{-\infty}^\infty \, e^{i (k - \beta)x} dx\right) \, d\beta \\
& = & \int_{-\infty}^\infty F(\beta) \, 2\pi \, \delta(k-\beta) \\
& = & 2\pi\, F(k).
\end{eqnarray*}
$$
In the first line I just swapped the order of integration. In the second line I just used the fact that the Fourier transform of $1$ is $2\pi\, \delta$ (more on that below). In the third line I used the sifting property of the delta function which holds as long as $F$ is continuous at $k$; this sifting property is often how delta functions are defined by most non-rigorous applied treatments. What steps are you having trouble with?

Note that we are using generalized functions (distributions) such as the delta function, and as such the integral symbols do not mean the same thing that they did when you learned calculus. When we write $\int e^{ikx} dx = 2\pi \delta(k)$ it we are simply saying that in the sense of generalized functions the Fourier transform of $1$ is $\delta$, we are not evaluating the integral as written (indeed, the integral as written diverges).

EDIT: note that the example I gave is just a statement that when you do the Fourier transform then the inverse Fourier transform of a function $F$ that you get to the original function. You can actually arrive at that conclusion using no delta functions at all.

Jason

 

[chiraganand]

You haven't given us enough information to make sense out of (8). What are $d$, $b$ and $\alpha$? Also, your first equation has no $x$ in it at all, only $\tilde{x}$ and $\tilde{x}^\prime$. I don't actually want you to answer these questions, by the way.

To me this looks like the kind of integral you get when are using Fourier analysis to solve PDEs. What you need to understand is the basic idea, then your specific integral will be up to you. Consider
$$
\begin{eqnarray*}
\int_{-\infty}^\infty \int_{-\infty}^\infty \, F(\beta) e^{i (k - \beta)x} d\beta\, dx
& = &
\int_{-\infty}^\infty F(\beta) \left( \int_{-\infty}^\infty \, e^{i (k - \beta)x} dx\right) \, d\beta \\
& = & \int_{-\infty}^\infty F(\beta) \, 2\pi \, \delta(k-\beta) \\
& = & 2\pi\, F(k).
\end{eqnarray*}
$$
In the first line I just swapped the order of integration. In the second line I just used the fact that the Fourier transform of $1$ is $2\pi\, \delta$ (more on that below). In the third line I used the sifting property of the delta function which holds as long as $F$ is continuous at $k$; this sifting property is often how delta functions are defined by most non-rigorous applied treatments. What steps are you having trouble with?

Note that we are using generalized functions (distributions) such as the delta function, and as such the integral symbols do not mean the same thing that they did when you learned calculus. When we write $\int e^{ikx} dx = 2\pi \delta(k)$ it we are simply saying that in the sense of generalized functions the Fourier transform of $1$ is $\delta$, we are not evaluating the integral as written (indeed, the integral as written diverges).

EDIT: note that the example I gave is just a statement that when you do the Fourier transform then the inverse Fourier transform of a function $F$ that you get to the original function. You can actually arrive at that conclusion using no delta functions at all.

Jason

Thank you for your reply and explanation. I kind of understand it now. I am more familiar with basic calculus, so i was wondering about how the delta function is introduced and why. I still have to get my head around these generalized functions and their intuitive meaning and how to actually evaluate and integral with these functions. Suppose I had just had a single integral which ends with the delta function, then what does it mean in terms of calculations or coding or numbers. I am sorry if its a dumb question.

 

[jasonRF]

Suppose I had just had a single integral which ends with the delta function, then what does it mean in terms of calculations or coding or numbers. I am sorry if its a dumb question.

There usually isn't much to do with a delta function by itself - what is usually most important about it is how it behaves when multiplied by a "nice" function and "integrated." Sometimes you may have an expression with multiple delta functions, or a delta function and some other stuff, and the coefficients in front of the deltas may give you information you want.

One thing to note is that you cannot actually actually evaluate a delta "function" at a point, so directly numerically evaluating them cannot be done. However, there are still instances where you can make a plot that represents the model. The simplest way is to use vertical arrows to represent the delta functions (see the first plot on the wikipiedia page: https://en.wikipedia.org/wiki/Dirac_delta_function), where the height of the arrow is the coefficient in front of the delta.

There are other options, too. For example, if we have a nice analytical model for a power spectrum that includes a delta function and some other stuff, one way to make a plot is to basically simulate the way a spectrum analyzer works. This means you pick a measurement bandwidth which sets up frequency bins, then you integrate the analytical model over each of those frequency bins to obtain the value of the spectrum that you plot for that bin.

Jason