Integration by residual theorem

[AlonsoMcLaren]

Homework Statement

Integrate $$\int_{-\infty}^{\infty} dx \ x^{-3}(sin x -x )$$

Homework Equations

Residual theorem, Jordan's lemma

The Attempt at a Solution

$$\int_{-\infty}^{\infty} dx \ x^{-3}(sin x -x ) = I am \ (PV\int_{-\infty}^{\infty} dx \ x^{-3}(e^{ix} -ix ))$$

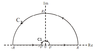
In the contour, if we let R goes to infinity and ρ goes to zero, then we have

$$\oint_{Total}^{ } dz \ z^{-3}(e^{iz} -iz) = \int_{C_{1}}^{ } dz \ z^{-3}(e^{iz} -iz) + \int_{C_{2}}^{ } dz \ z^{-3}(e^{iz} -iz) + PV \int_{-\infty}^{\infty} dx \ x^{-3}(e^{ix} -ix)$$

Because the only singularity is 0, not inside the contour. By residual theorem (or Cauchy's theorem),
$$\oint_{Total}^{ } dz \ z^{-3}(e^{iz} -iz) = 0$$

By Jordan's lemma, as R goes to infinity,

$$\int_{C_{2}}^{ } dz \ z^{-3}(e^{iz} -iz) =0$$

For the C1 contour

$$\int_{C_{1}}^{ } dz \ z^{-3}(e^{iz} -iz)= \int_{\pi}^{0 } d(\rho e^{i\theta }) \frac{e^{i\rho e^{i\theta }} -i\rho e^{i\theta }}{(\rho e^{i\theta })^{3}}= i \int_{\pi}^{0 }\frac{e^{i\rho e^{i\theta }}-i\rho e^{i\theta}}{\rho ^{2}e^{2i\theta }} d \theta$$

But as ρ goes to 0, $$\frac{e^{i\rho e^{i\theta }}-i\rho e^{i\theta}}{\rho ^{2}e^{2i\theta }}$$

goes to infinity. So I am stuck.

The final answer, according to WolframAlpha, is -π/2

 

[jackmell]

\frac{e^{i\rho e^{i\theta }}-i\rho e^{i\theta}}{\rho ^{2}e^{2i\theta }} [/tex]

goes to infinity.

No.

Your mission, should you choose to accept it, is to show:

$$\lim_{\rho\to 0} \int_{\pi}^{0}\frac{e^{i\rho e^{it}}-i\rho e^{it}}{\rho^2 e^{2 i t}} dt =\pi/2$$

and you can't just say it is cus' I told you so because I could be wrong. I've not been able to do so myself yet. Ain't that the fun part of math?

Edit: Ok, I think I have it. Kinda' rickety and not sure about the legitimacy of applying L'Hopital's rule to integral functions but it's something. You try to get it and let me know what you get.

 

[jackmell]

No.

Your mission, should you choose to accept it, is to show:

$$\lim_{\rho\to 0} \int_{\pi}^{0}\frac{e^{i\rho e^{it}}-i\rho e^{it}}{\rho^2 e^{2 i t}} dt =\pi/2$$

and you can't just say it is cus' I told you so because I could be wrong. I've not been able to do so myself yet. Ain't that the fun part of math?

Edit: Ok, I think I have it. Kinda' rickety and not sure about the legitimacy of applying L'Hopital's rule to integral functions but it's something. You try to get it and let me know what you get.

A PF member was kind enough to help me with a part of this analysis in the Calculus sub-forum and according to his analysis, I am justified in applying L'Hopital's rule under the integral sign in this particular case:

https://www.physicsforums.com/showthread.php?p=4531822&posted=1#post4531822

Fun problem. Thanks voko!

 

[brmath]

It is clear that the original integral converges since $x^{-3}$ will govern. And I suppose you are taking a course in complex variables and are supposed to use contour integrals.

But in a contrarian spirit, allow me to suggest that you can find an antiderivative for this integrand. Integrate by parts several times.

And in an inquiring spirit, could you enlighten me as to what PV means. I know the Cauchy Integral formula but have not seen the notation PV.

Re applying L'Hospital's theorem, that theorem is just expressing some facts about the Taylor's polynomial. No reason why you can't expand your function under an integral sign (we do it all the time).

 

[Office_Shredder]

But in a contrarian spirit, allow me to suggest that you can find an antiderivative for this integrand. Integrate by parts several times.

How would you do this? I assume you intend to integrate the x^-3 but when you run into a log you are going to be in trouble.

And in an inquiring spirit, could you enlighten me as to what PV means. I know the Cauchy Integral formula but have not seen the notation PV.

It means principal value, and means instead of taking the true double sided limit you take
$$\lim_{R\to \infty} \int_{-R}^{R}$$
which is what you actually get when you do contour integration (meaning you can do contour integration to calculate the principal value of something where the true integral doesn't exist). If the integral converges then it converges to the same value as the principal value of course.

 

[AlonsoMcLaren]

No.

Your mission, should you choose to accept it, is to show:

$$\lim_{\rho\to 0} \int_{\pi}^{0}\frac{e^{i\rho e^{it}}-i\rho e^{it}}{\rho^2 e^{2 i t}} dt =\pi/2$$

But $$\lim_{\rho\to 0} \int_{\pi}^{0}\frac{e^{i\rho e^{it}}-i\rho e^{it}}{\rho^2 e^{2 i t}} dt =\pi/2$$ is indeed infinity

If you do taylor expansion:

$$e^{i\rho e^{it}} = 1+ i\rho e^{it}-\frac{1}{2}\rho^{2} e^{2it}+...$$

$$e^{i\rho e^{it}}-i\rho e^{it} = 1-\frac{1}{2}\rho^{2} e^{2it}+...$$

$$\frac{e^{i\rho e^{it}}-i\rho e^{it}}{\rho^2 e^{2 i t}} = \rho^{-2}e^{-2it}-1/2+..$$

It blows up as ρ goes to zero!

 

[brmath]

How would you do this? I assume you intend to integrate the x^-3 but when you run into a log you are going to be in trouble.



It means principal value, and means instead of taking the true double sided limit you take
$$\lim_{R\to \infty} \int_{-R}^{R}$$
which is what you actually get when you do contour integration (meaning you can do contour integration to calculate the principal value of something where the true integral doesn't exist). If the integral converges then it converges to the same value as the principal value of course.

Sorry about my contrarian spirit, which both saw that the $x^{-3}$ would govern, and viewed it as $x^3$ for integration purposes. This is too contrarian even for me.

I've used lim$\int_{-R}^R$ in contour integration, but didn't know it was called the Principal Value.

 

[jackmell]

But $$\lim_{\rho\to 0} \int_{\pi}^{0}\frac{e^{i\rho e^{it}}-i\rho e^{it}}{\rho^2 e^{2 i t}} dt =\pi/2$$ is indeed infinity

If you do taylor expansion:

$$e^{i\rho e^{it}} = 1+ i\rho e^{it}-\frac{1}{2}\rho^{2} e^{2it}+...$$

$$e^{i\rho e^{it}}-i\rho e^{it} = 1-\frac{1}{2}\rho^{2} e^{2it}+...$$

$$\frac{e^{i\rho e^{it}}-i\rho e^{it}}{\rho^2 e^{2 i t}} = \rho^{-2}e^{-2it}-1/2+..$$

It blows up as ρ goes to zero!

Outstanding Alonso. I see you've completed your mission and taught me a very simple way to show the limit:

$$\begin{align*} \lim_{\rho\to 0}\int_{\pi}^0 \frac{e^{i\rho e^{it}}- i\rho e^{it}}{\rho^2 e^{it}}dt&=\lim_{\rho\to 0}\int_{\pi}^0 \left(-\frac{1}{2}+\frac{e^{-2 i t}}{\rho ^2}-\frac{1}{6} i e^{i t} \rho +\frac{1}{24} e^{2 i t} \rho ^2+\frac{1}{120} i e^{3 i t} \rho ^3+\cdots\right)dt \\ &=\pi/2+\lim_{\rho\to 0} \frac{1}{\rho^2}\int_{\pi}^0 e^{-2 i t}dt+0 \\ &=\pi/2+\lim_{\rho\to 0} \frac{1}{\rho^2}(0)+0 \\ &=\pi/2 \end{align*}$$