ing_it
- 27
- 1
Homework Statement
We have a wire of the length L=0.2m which is uniformly charged with a linear density of Lambda = 3nC/cm.
Find the intensity (E) of the electric field in point A1 whose perpendicular distance from the wire is a=0.05m.
The wire is in a vacuum.
Compare the intensity with the intensity you calculate through Gauss' Law and explain any differences in your answers.
Homework Equations
I will be using h in my calculations. h=L. I just used it because it's easier to think about a cylinder while using h.
No Gauss law:
E = {\frac {Q}{4 \pi \epsilon_0 r^2}}
Q = \lambda h
With Gauss' law.
\phi= {\frac {Q}{\epsilon_0}}
\phi = E \cdot S_{surface}
Q= \lambda h<br /> <h2>The Attempt at a Solution</h2><br /> Please look at the picture I added. I have the problem drawn out there.<br /> <br /> First I'm going to use Gauss' law because I feel like I've got that one right (but I might just feel that way and will end up way off)<br /> \phi = \oint _S \vec{E} \cdot \vec{dS} = \int_{base1} \vec{E} \cdot \vec{dS} + \int_{base2} \vec{E} \cdot \vec{dS} + \int_{surface} \vec{E} \cdot \vec{dS} = \int_{base1} E dS cos {\frac{\pi}{2}} + \int_{base2} E dS cos {\frac{\pi}{2}} + \int_{surface} E dS cos 0 = E \int_{surface} dS = ES_{surface}<br /> since<br /> \phi = E \cdot S_{surface} and \phi= {\frac {Q}{\epsilon_0}}<br /> then<br /> E \cdot S_{surface} = {\frac{Q}{\epsilon_0}}<br /> E 2 \pi a h = {\frac{\lambda h}{\epsilon_0}}<br /> E = {\frac{\lambda}{2 \pi \epsilon_0 a}}<br /> Is this part correct?<br /> <br /> And then onto the part where I'm not so sure. <br /> I started out with the same thing as above.<br /> \phi = \oint _S \vec{E} \cdot \vec{dS} = \int_{base1} \vec{E} \cdot \vec{dS} + \int_{base2} \vec{E} \cdot \vec{dS} + \int_{surface} \vec{E} \cdot \vec{dS} = \int_{base1} E dS cos {\frac{\pi}{2}} + \int_{base2} E dS cos {\frac{\pi}{2}} + \int_{surface} E dS cos 0 = E \int_{surface} dS = ES_{surface}<br /> \phi = E S_{surface} = E 2 \pi a h<br /> But once I got to this point I didn't use Gauss' law (I hope. We used this in class before we started using Gauss' law so I hope it's not just some variation of it) I substituted this for my E in "phi = E S<sub>surface</sub>" :<br /> E = {\frac {Q}{4 \pi \epsilon_0 a^2}}<br /> \phi = {\frac {Q}{4 \pi \epsilon_0 a^2}} 2 \pi a h = {\frac{Qh}{2 \epsilon_0}}<br /> I plugged in<br /> Q = \lambda h<br /> So I got<br /> \phi = {\frac{\lambda h^2}{2 \epsilon_0}}<br /> And then I again used E.S = phi<br /> E 2 \pi a h ={\frac{\lambda h^2}{2 \epsilon_0}}<br /> E = {\frac{\lambda h}{4 \pi a \epsilon_0}}<br /> It seems a bit too easy and I'm pretty sure that when something like this seems easy, there must be a mistake.<br /> <br /> And as to what I think of the differences: through Gauss' law, the length of the wire does not factor into the equation, so it might be okay if we're thinking of some theoretical, endless wire, but for a wire of finite length the method that does not use Gauss' law should be more precise.<br /> The difference between my equation and Gauss' law is that my equation has an added h/2. But why are we only counting with only half the length of the wire I do not know.
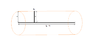
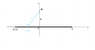
 I'll work on that. :D
I'll work on that. :D 
