Interference - two waves of different frequencies - beat velocity

[LmdL]

Hello,
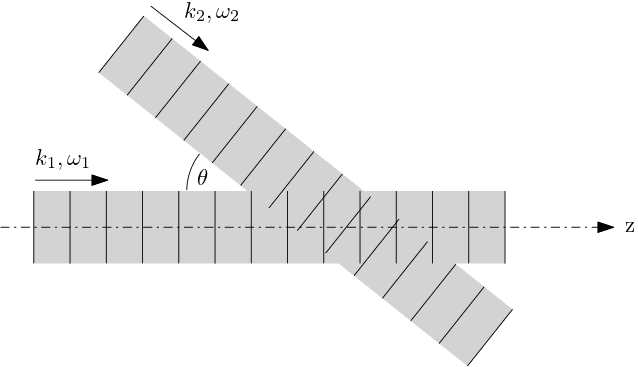
I'm considering the "beats" phenomena. I have two plane waves in some medium with a refractive index n(ω), one propagates in a z direction and second in a direction making an angle θ with z axis. Waves have frequencies ω₁, ω₂ (not necessarily equal) and k-vectors k₁, k₂ (not necessarily equal):

Now, I'm interested in interference (in the area where both waves overlap) along the z axis direction. I can write the initial fields contributions along the z axis as

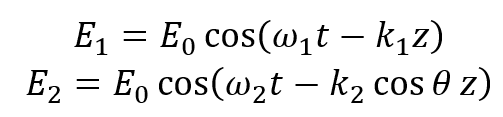
So their sum is

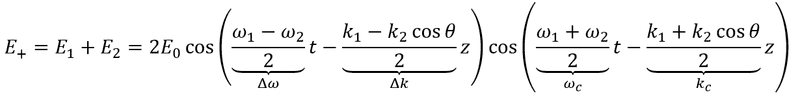
First cosine is the envelope modulation and second is the carrier wave. Now, my question is regarding the modulation speed. As far as I understand, the above describes the beats phenomena. Or, alternatively, an interference pattern with a period of 2π/Δk that moves in time. If I'm right, the modulation speed reads

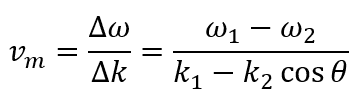
And here is the question: this speed can exceed c (speed of light), once I change the θ. For some θ I can even get an infinite v_m (when denominator vanishes). On the other hand, modulation speed should be limited by the speed of light. What I'm missing here?
The possibilities that I thought of:
1. This modulation speed is a sinusoidal and cannot transfer any information, thus isn't limited by c.
2. The expression for v_m is correct, but for values of θ that lead to v_m>c it should be constrained v_m=c .
3. The expression for v_m is an expression for phase velocity and I should use d(Δω)/d(Δk) instead (group velocity). However, in this case I also get velocities that exceed c (checked numerically).

Any advice or thoughts are appreciated.
Thank you.

 

[andrewkirk]

The modulation speed need not be limited by c because it is not the speed of a particle or wave. It is the speed of a feature in a pattern, which is an abstract, non-physical concept, and hence not limited by the speed of light.
As another example of how this can happen, consider a powerful, perfect laser mounted perpendicularly on an axle in the middle of a sphere with radius one light second and pointing directly at the sphere's inner surface. The laser rotates on the axle at a rate of one full rotation per 3 seconds, so that the dot of light it makes on the sphere's inner surface traverses a full equatorial circle of the sphere in that time - distance covered = 2 pi light seconds - more than twice the speed of light. Yet the laser itself is only moving quite slowly. This can happen because the only thing moving on the sphere's inner surface is a feature in a pattern - not a physical thing limited by c.

 

[LmdL]

Thank you for your reply. I got your point. I have an additional question: let's suppose I place a particle on the z axis (in the waves overlapping area) and restrict it to move along z axis, for example by adding two transparent parallel to z axis plates, one slightly above it and one slightly below. Particle is then confined to one of the modulation wave maxima (similar to optical tweezers). What will happen now? I suppose that if v_m is below c, the particle will move with that speed along the z axis, being in the area of the modulation maximum it was confined to from the beginning. What if v_m>c? Particle will "slip" to the next maximum to the left, and then again, and again, and so forth? Is this correct?

 

[andrewkirk]

Why would the particle move at all? What force are you expecting to act on the particle to accelerate it out of a stationary state?

 

[LmdL]

Never mind. I need to review my understading of optical tweezers. Thank you for your help!