Intersection between rotated & translated ellipse and line

[piercazzo]

I have a rotated ellipse, not centered at the origin, defined by x,y,a,b and angle.
Then I have a segment defined by two points x1,y1 and x2,y2
Is there a quick way to find the intersection points?

I used wolfram alpha equation solver, I tried to insert the equation of a line into the one of a standard non rotated, non translated ellipse,

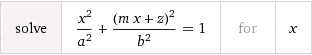
and resolving for x this is the result

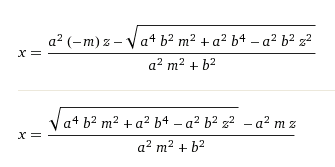
which is nice.

Then I took the equation of a rotated and translated ellipse

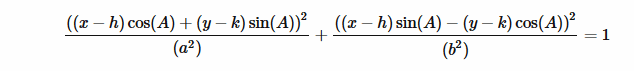
and this is the result

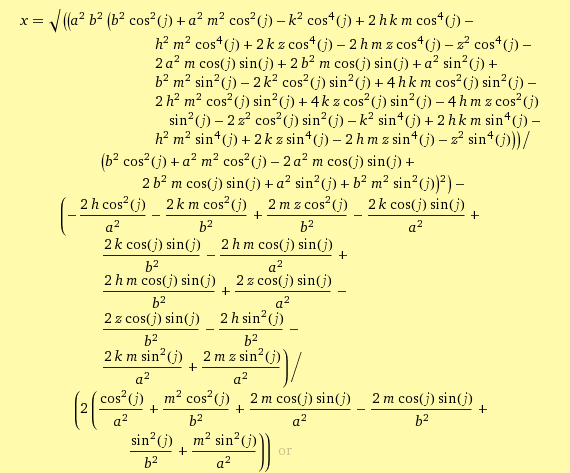
Which is obviously impractical, can anyone suggest a different method?

 

[Simon Bridge]

Do it by hand rather than use the calculator.
You can either -
1. Solve for one variable in the line equation and sub into the ellipse equation - solve for the other coordinate ... you know: as usual.

2. transform the ellipse into standard form, apply the same transformation to the line, find solutions for the transformed system, apply the inverse transformation to the solution.