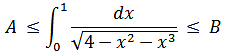Interval of the Riemann integral value

Click For Summary
SUMMARY

The discussion focuses on finding the interval of the Riemann integral for the function $\tfrac1{\sqrt{4-x^2-x^3}}$ over the range $0 \leq x \leq 1$. Participants confirm that the function is increasing within this interval, with a minimum value at $x=0$ and a maximum at $x=1$. The integral is established to be greater than 0, reinforcing the conclusion that the estimates for the integral's bounds, A and B, can be derived from these values.

PREREQUISITES
  • Understanding of Riemann integrals
  • Knowledge of calculus, specifically integration techniques
  • Familiarity with function behavior and monotonicity
  • Basic algebra for manipulating expressions
NEXT STEPS
  • Study Riemann integral properties and applications
  • Explore techniques for estimating integrals of increasing functions
  • Learn about the behavior of functions under square root transformations
  • Investigate numerical methods for approximating definite integrals
USEFUL FOR

Mathematicians, calculus students, and anyone interested in understanding Riemann integrals and their applications in estimating function behavior.

goody1
Messages
16
Reaction score
0
Hello everyone, I have to find an interval of this Riemann integral. Does anybody know the easiest way how to do it? I think we need to do something with denominator, enlarge it somehow. My another guess is the integral is always larger than 0 (A=0) because the whole function is still larger than 0 on interval from 0 to 1. Thank you in advance.
 

Attachments

  • integral.png
    integral.png
    1 KB · Views: 126
Physics news on Phys.org
The function $\tfrac1{\sqrt{4-x^2-x^3}}$ increases on the interval $0\leqslant x\leqslant 1$. The minimum value occurs when $x=0$, and the maximum at $x=1$. You can use that to get estimates for $A$ and $B$.
 
Opalg said:
The function $\tfrac1{\sqrt{4-x^2-x^3}}$ increases on the interval $0\leqslant x\leqslant 1$. The minimum value occurs when $x=0$, and the maximum at $x=1$. You can use that to get estimates for $A$ and $B$.
I tried this. Is that corect solution?
 

Attachments

  • inn.png
    inn.png
    1.2 KB · Views: 150
goody said:
I tried this. Is that corect solution?
Yes, that is what I had in mind. :)
 

Similar threads

MHB Improper integral of an even function
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Is my interpretation of this three dimensional improper integral correct?
  • · Replies 4 ·
Replies
4
Views
2K
Graduate Disjoint intervals for Riemann Integral
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Infinite Series - Divergence of 1/n question
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Definitions of the Riemann integral
  • · Replies 14 ·
Replies
14
Views
3K
Undergrad Original definition of Riemann Integral and Darboux Sums
  • · Replies 14 ·
Replies
14
Views
4K
Undergrad Riemann integrability with a discontinuity
  • · Replies 10 ·
Replies
10
Views
4K
MHB Finding an Integral for a given Riemann Sum
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Riemann integrability and uniform convergence
  • · Replies 2 ·
Replies
2
Views
3K
MHB Find a formula for the Riemann sum and take the limit of the sum as n->infinite
  • · Replies 1 ·
Replies
1
Views
4K