warhammer
- 164
- 33
- Homework Statement
- Q1 (i) Given φ(k) = \frac{A/Δk} where (k0 − 0.5Δk)< k < (k0 +0.5Δk) & φ(k) is 0 elsewhere. A, k0 and Δk are constants.
Show that ψ(x) = A * \frac{sinb/b} *exp(ik0x) where b =0.5Δkx. Also find ψ(0).
(ii) A particle freely moves in an one dimensional box of length L. The probability of finding the particle between x and x + dx inside the box is P(x)dx = Cdx, 0 ≤ x ≤ L where C is a constant. It is 0 elsewhere. Find C, < x > and < x^n >
- Relevant Equations
- ψ(x)= \frac{1/√(2pi)} \int_-∞^∞ φ(k) exp(ikx) dx\
<expectation value of an observable>= \int ψ(x)*(observable)ψ(x)
Below I have attached an image of my possible solution. I have replaced all the relevant limits. For some reason, I am getting the final value for (i) part as ψ(x)= with an additional √2pi in the denominator. Have I made any errors or is it fine if I take it within the constant A..
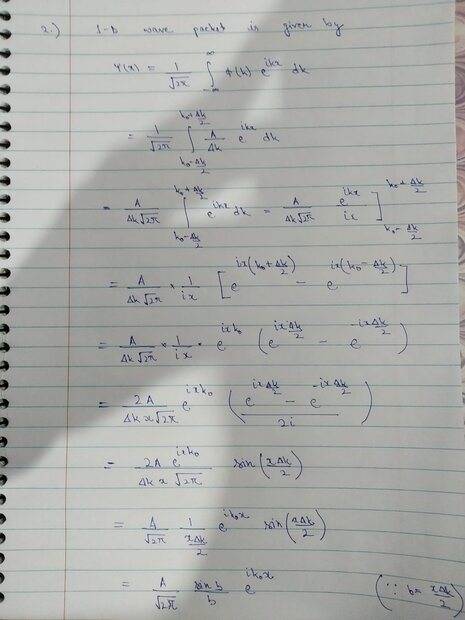
In addition I have also posted images of the solution for the (ii) part where I am obtaining ψ(0)=0 and the expectation values. I shall be extremely indebted if someone can have a look at my solutions and verify if they are fine, or otherwise, graciously provide guidance so that I may be able to correct them.
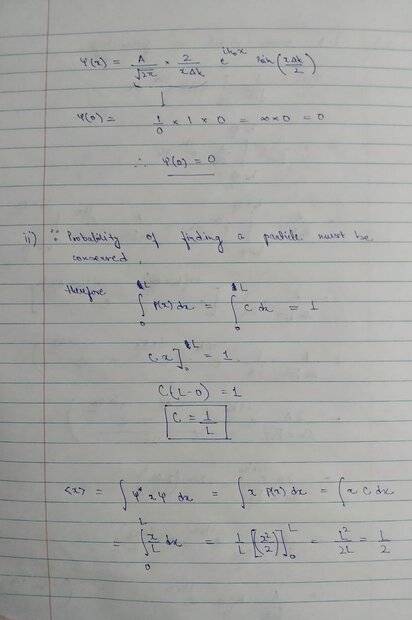
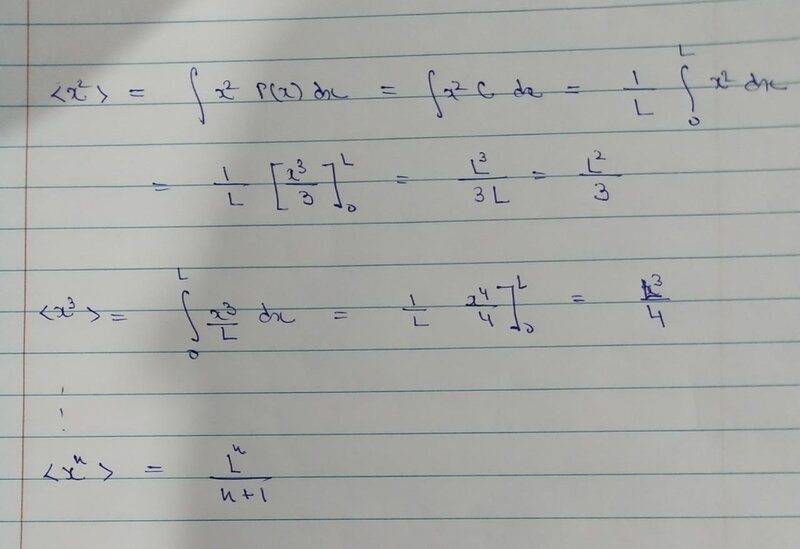
In addition I have also posted images of the solution for the (ii) part where I am obtaining ψ(0)=0 and the expectation values. I shall be extremely indebted if someone can have a look at my solutions and verify if they are fine, or otherwise, graciously provide guidance so that I may be able to correct them.