Intuitive meaning of Dot Product

[22990atinesh]

I know intuitively that the Cross Product of two vectors $\vec{A}$ and $\vec{B}$ represents another vector $\vec{A \times B}$ perpendicular to it. In study of physics we come across this situation a lot. Hence I can visualize some applications of it

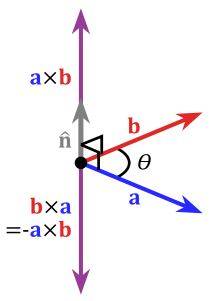
I know that the dot product of two vectors $\vec{A}$ and $\vec{B}$ is scalar quantity and also that it represents angular relationship between $\vec{A}$ and $\vec{B}$ .i.e.

• If $\vec{A}$.$\vec{B} = 0$. Then $\vec{A}$ and $\vec{B}$ are perpendicular.

• If $\vec{A}$.$\vec{B} > 0$ (Positive). Then the angle between $\vec{A}$ and $\vec{B}$ are less than $90^o$.

• If $\vec{A}$.$\vec{B} < 0$ (Negative). Then the angle between $\vec{A}$ and $\vec{B}$ are greater than $90^o$.

But I won't be able to understand intuitively, What does the dot product represents. What does the magnitude of the dot product of two vectors represents.

 

[jtbell]

It represents the component or projection of one vector along the other one, times the magnitude of the other one. This diagram shows it using the projection of A along B: (|A| cos θ)|B|.

You can also do it the other way, using the projection of B along A, and get the same result: (|B| cos θ)|A|.

 

[A.T.]

I know intuitively that the Cross Product of two vectors $\vec{A}$ and $\vec{B}$ represents another vector $\vec{A \times B}$ perpendicular to it.

But that's not all. The magnitude of the cross product also has a geometrical interpretation:

But I won't be able to understand intuitively, What does the dot product represents. What does the magnitude of the dot product of two vectors represents.

What baffles me, is that you obviously found the wiki page on the cross product (and posted the picture from it), but couldn't find the page on the dot product with the picture jtbell posted.

 

[22990atinesh]

It represents the component or projection of one vector along the other one, times the magnitude of the other one. This diagram shows it using the projection of A along B: (|A| cos θ)|B|.

You can also do it the other way, using the projection of B along A, and get the same result: (|B| cos θ)|A|.

But that's not all. The magnitude of the cross product also has a geometrical interpretation:

...

What baffles me, is that you obviously found the wiki page on the cross product (and posted the picture from it), but couldn't find the page on the dot product with the picture jtbell posted.

I've read that article. I understand that the multiplication of the projection of $\vec{a}$ onto $\vec{b}$ (|$\vec{a}$|cos θ) with |$\vec{b}$| gives the dot product of vectors $\vec{a}$ and $\vec{b}$. But my doubt is that, what does this quantity represents. Whats the application of it.

 

[jtbell]

Have you studied the concept of "work" in physics yet? That's the first application of the dot product that most physics students see.