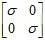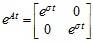SUMMARY
The discussion centers on the necessity of diagonalizability for computing the matrix exponential of a matrix A. It is established that while A does not need to be simple (having distinct eigenvalues), it must be diagonalizable to compute its exponential accurately. The matrix exponential is defined through a series expansion, and the transformation f(A) = U-1 f(D) U is crucial, where D is a diagonal matrix of eigenvalues. The eigenvectors of A must be linearly independent for A to be diagonalizable, which is essential for the computation of the exponential function.
PREREQUISITES
- Understanding of matrix diagonalization
- Familiarity with eigenvalues and eigenvectors
- Knowledge of analytic functions and series expansions
- Basic concepts of matrix exponentiation
NEXT STEPS
- Study the process of matrix diagonalization in detail
- Learn about the implications of repeated eigenvalues on diagonalizability
- Explore the series expansion of analytic functions, particularly in the context of matrices
- Investigate the convergence properties of the matrix exponential series
USEFUL FOR
Mathematicians, engineers, and students in linear algebra or applied mathematics who are working with matrix computations and need to understand the conditions for diagonalizability and matrix exponentiation.