Is Entropy decreased for Free expansion of a Waals gas?

[Astrocyte]

Homework Statement

What is the change in entropy of van der Waals gas in free expansion?
Free expansion from V to 2V

Relevant Equations

(p+aN^2/V^2)(V-Nb)=NkT

Previous of this problem, there was another problem. that is "What is the change in Temperature of van der Waals gas in free expansion?".
I got them.
It was
C_V dT= -aN^2/V^2 dV
Then, I got
T=T0-aN^2/2VC_V
So i knew that the Temperature is decreased by free expansion in adiabatic process.
Then I calculated some about the change of entropy.

And I notice that this result says "entropy can be decreased for Free expansion of Waals gas.
What did i do wrong for this calculation?

 

[Chestermiller]

I get something similar, solving it a very different way, and working in terms of specific volume v and specific entropy s: $$\Delta s=C_v\ln{\left(1-\frac{a}{2vT_0C_v}\right)}+R\ln{\left(\frac{2v-b}{v-b}\right)}$$where Cv is independent of v and T, and thus equal to the heat capacity in the ideal gas limit.

 

[TSny]

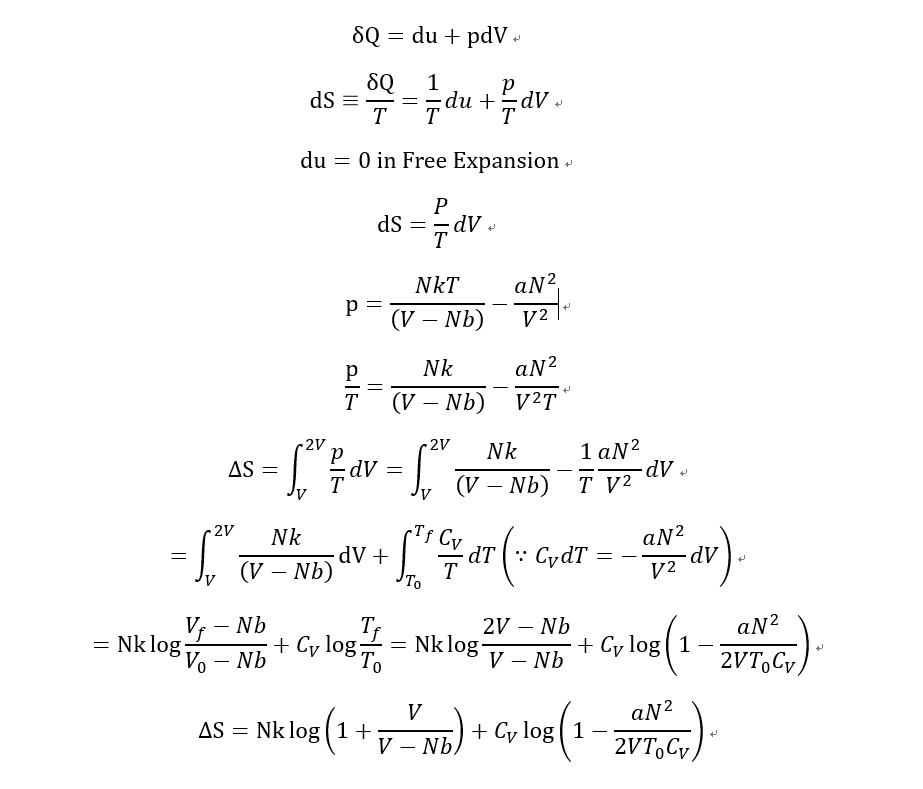
And I notice that this result says "entropy can be decreased for Free expansion of Waals gas.
What did i do wrong for this calculation?

I don't think you did anything wrong. From $\Delta S = \int_V^{2V}\frac{P}{T}dV$, you can see that $\Delta S$ must be positive since $P$, $T$, and $V$ are positive. The fact that $P$ is positive, means that in the equation $P = \frac{NkT}{V-Nb} - \frac{aN^2}{V^2}$, the first term on the right "outweighs" the second term on the right. These two terms lead to the two terms in your final result $$\Delta S = Nk \log \left (1+ \frac{V}{V-Nb} \right)+C_V\log \left (1- \frac{aN^2}{2VT_0C_V} \right)$$

So, although the second term in the result is negative, the overall expression must be positive.

 

[Chestermiller]

My analysis was based on the following equations for an arbitrary fluid:
$$ds=\left(\frac{\partial s}{\partial T}\right)_vdT+\left(\frac{\partial s}{\partial v}\right)_Tdv$$with $$\left(\frac{\partial s}{\partial T}\right)_v=\frac{C_v}{T}$$and$$\left(\frac{\partial s}{\partial v}\right)_T=\left(\frac{\partial P}{\partial T}\right)_v$$For a van der Waals gas, the latter equation reduces to:$$\left(\frac{\partial s}{\partial v}\right)_T=\frac{R}{(v-b)}$$These equations imply that Cv depends only on T.

 

[Astrocyte]

So, although the second term in the result is negative, the overall expression must be positive.

I understood it. Thank you.
Temperature T is always positive and P is also positive. So, the integration must be positive.
In my result, the second term will be negative. But, the size of negative term is not big enough to exceed the first term.
I should check with graph.

 

[Astrocyte]

My analysis was based on the following equations for an arbitrary fluid:
$$ds=\left(\frac{\partial s}{\partial T}\right)_vdT+\left(\frac{\partial s}{\partial v}\right)_Tdv$$with $$\left(\frac{\partial s}{\partial T}\right)_v=\frac{C_v}{T}$$and$$\left(\frac{\partial s}{\partial v}\right)_T=\left(\frac{\partial P}{\partial T}\right)_v$$For a van der Waals gas, the latter equation reduces to:$$\left(\frac{\partial s}{\partial v}\right)_T=\frac{R}{(v-b)}$$These equations imply that Cv depends only on T.

Did you use The Maxwell relation? I know about the name. but I'm not learn about that yet.
But, I think the relation makes other problem very easy.

 

[Chestermiller]

Did you use The Maxwell relation?

Yes