Finding the increase in entropy of the universe in gas expansion

[lorenz0]

Homework Statement

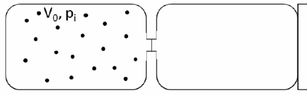
Two boxes of equal volume $V_0$ are separated by a membrane. The first one to the left, thermally isolated contains $n$ moles of perfect biatomic gas at pressure $p_i$ and temperature $T_i$. The second box is empty, and in contact with a source of heat at a temperature which is $T_i/2$. At a certain instant the membrane is removed and the gas reaches a new equilibrium. Find: a) the final pressure of the gas $P_f$ b) the heat $Q$ exchanged with the source of heat c) the variation of entropy of the universe $\Delta U_{univ}$

Relevant Equations

$PV=nRT, \Delta U=nC_V \Delta T=Q-L, \Delta S=nC_V \ln(\frac{T_f}{T_i})+nR\ln(\frac{V_f}{V_i})$

a) $P_f=\frac{nRT_f}{V_f}=\frac{nR\frac{T_i}{2}}{2V_0}=\frac{1}{4}\frac{nRT_i}{V_0}=\frac{1}{4}P_i$

b) $Q=\Delta U=nC_V \Delta T=n\frac{5}{2}R(-\frac{T_i}{2})=-\frac{5}{4}nRT_i=-\frac{5}{4}P_i V_0$ ($L=0$ since the gas expands in a vacuum;Now, (a) and (b) are both correct but not (c), for which I get:c) $\Delta S_{system}=nC_V \ln(\frac{T_f}{T_i})+nR\ln(\frac{V_f}{V_i})=n\frac{5}{2}R\ln(\frac{\frac{T_i}{2}}{T_i})+nR\ln(\frac{2V_0}{V_0})=-\frac{3}{2}nR\ln(2)$ I understand that the entropy of the system decreases since heat goes out of the system so I guessed that the entropy of the universe should go up by the same amount but apparently this is wrong as in the solution given in the text is $n\frac{5}{2}R-\frac{3}{2}nR\ln(2)$. What is it that I am missing in finding the entropy of the universe? How should I reason about such a problem in general? Thanks

 

[Chestermiller]

The surroundings is being treated as an ideal constant temperature reservoir at temperature $T_i/2$. The amount of heat it receives at this temperature is $+\frac{5}{4}nRT_i$. So what is its entropy change?

Otherwise, you did a great job of analyzing this.

 

[lorenz0]

The surroundings is being treated as an ideal constant temperature reservoir at temperature $T_i/2$. The amount of heat it receives at this temperature is $+\frac{5}{4}nRT_i$. So what is its entropy change?

It is $\frac{Q}{T_i /2}=\frac{\frac{5}{4}nRT_i}{\frac{T_i}{2}}=\frac{2}{T_i}\frac{5}{4}nRT_i=\frac{5}{2}nR$ so $\Delta S_{universe}=\frac{5}{2}nR-\frac{3}{2}nR\ln(2)=\frac{nR}{2}(5-3\ln(2))$. So the entropy change of the universe is the sum of the entropy change of the system + entropy change of its surroundings, right?

 

[Chestermiller]

It is $\frac{Q}{T_i /2}=\frac{\frac{5}{4}nRT_i}{\frac{T_i}{2}}=\frac{2}{T_i}\frac{5}{4}nRT_i=\frac{5}{2}nR$ so $\Delta S_{universe}=\frac{5}{2}nR-\frac{3}{2}nR\ln(2)=\frac{nR}{2}(5-3\ln(2))$. So the entropy change of the universe is the sum of the entropy change of the system + entropy change of its surroundings, right?

Yes. Very nice.

 

[lorenz0]

Yes. Very nice.

You have been very helpful: thanks!