Is it possible for a low pass filter to have such a transfer function?

[arhzz]

Homework Statement

Find the transfer function

Relevant Equations

Circuit analysis

Hello!

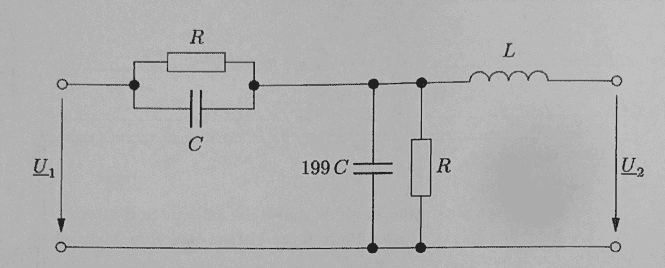
Consider this filter,and that I have to find the transfer function U2/U1 with the norm Ω= ωRC (also double fractions are not allowed)

Now I can see that that the resistor and capacitor left as well as right are parallel to each other. So simplifying that

$Z_1 = \frac{R}{jωRC +1}$ Where Z1 is the Impedance on the left.
$Z_2 = \frac{R}{jωR199C +1}$ Where Z2 the impedance on the middle, L is irrelevant since no current is flowing there ( the circuit is open)

Now I can simplify with the norm and use the voltage divider to find the transfer function (T)

$T(Ω) = \frac{Z_2}{Z_1+Z_2}$ Inputting this gives me a double fraction

Now since I cannot have a double fraction I multiply everything by jΩ199 +1 and I am left with this

$\frac{R}{\frac{Rj199Ω+R }{jΩ+1 }+R }$ Now I multiply by jΩ +1 and I am left with this

$\frac{R(jΩ +1)}{R(jΩ199+1)+R(jΩ +1)}$

So the final soultion should be $\frac{1+jΩ}{jΩ200 +2}$

Now I am not so sure that this is correct.The reason why is because the next part of the problem they want me to find out how the transfer function looks like when Ω = 0,and what type of filter this is(low pass high pass etc..). I get that it should be 1/2 but I am not so sure that this is valid.I think I am susposed to get 1,because a low pass filter has transfer function 1 (ideally) for when the frequency is really low (hence really close to 0).I am not familiar with a filter that has a transfer function 1/2 at Ω = 0. Is it possible that I made a mistake somewhere in the transfer function; I've checked it thorughly and I think its okay,that would mean that I am missing something.

Any insights? Thanks

 

[LvW]

Of course, there are lowpaas filters with a DC values smaller than 0 dB (or even larger in case of active devices).
But note, that your circuit (a) is not a "classical" lowpass approaching zero amplitudes for very large frequencies and (b) will have another response with a resistive termination (due to the inductance, which has no influence without such a termination).

 

[Baluncore]

Any insights? Thanks

Ignoring the capacitors. At low frequencies, the output will be R/(R+R) = 1/2 of the input.
Ignoring the resistors. At high frequencies, the capacitive divider will output about 1/200 of the input.

 

[arhzz]

Of course, there are lowpaas filters with a DC values smaller than 0 dB (or even larger in case of active devices).
But note, that your circuit (a) is not a "classical" lowpass approaching zero amplitudes for very large frequencies and (b) will have another response with a resistive termination (due to the inductance, which has no influence without such a termination).

Huh I did not know that such filter existed. So you would say that the transfer function is correct? And for b) I did not quite get what you meant with resistive termination? I know what it is but what has the inductance to do with it since the inductance should play no role,since there is no current there.Are you trying to say that the "behaviour" of the lowpass will be diffreent from the "classic" (that for very low frequencies,approaching 0 that it will have transfer function 0)?

 

[LvW]

I did not quite get what you meant with resistive termination? I know what it is but what has the inductance to do with it since the inductance should play no role,since there is no current there.

What is the purpose of a filter?
Answer: To process an incoming signal in a certain way - and to deliver the result to another device.
This device will have - in most cases - a finite input resistance which will allow a current through the inductor.
What else should be the reason to have such an inductor in the ciruit?
In your case it is just an open circuit - not very realistic.
That was the background of my remark.
The inductor - together with any resistive termination - will change the order of your circuit from n=2 to n=3; and the last stage (L-R) will cause the signal to go down to zero for very large frequencies.

 

[arhzz]

What is the purpose of a filter?
Answer: To process an incoming signal in a certain way - and to deliver the result to another device.
This device will have - in most cases - a finite input resistance which will allow a current through the inductor.
What else should be the reason to have such an inductor in the ciruit?
In your case it is just an open circuit - not very realistic.
That was the background of my remark.
The inductor - together with any resistive termination - will change the order of your circuit from n=2 to n=3; and the last stage (L-R) will cause the signal to go down to zero for very large frequencies.

Okay I see now. But here is the other thing. I have tried calculating the cutoff frequency of this filter (with this transfer function) and I get it is negative. That should be impossible,to have negative cutoff frequency.

Since I'm pretty sure that is wrong,where could the error be?

EDIT: Nevermind I made a calculation error. I get 0,01

 

[LvW]

EDIT: Nevermind I made a calculation error. I get 0,01

* OK - I see: You have calculated the normalized quantity Ω
* And HOW did you calculate ? Which definition did you apply?

 

[Delta2]

What does L do in the case we connect an output device to this filter so that current flows through L?

 

[Baluncore]

What does L do in the case we connect an output device to this filter so that current flows through L?

The inductor - together with any resistive termination - will change the order of your circuit from n=2 to n=3; and the last stage (L-R) will cause the signal to go down to zero for very large frequencies.

 

[Delta2]

Ok partially understood except from the "change the order of your circuit from n=2 to n=3" . Does it refer to the maximum order of the ODEs that describe the circuit?

 

[Baluncore]

https://eng.libretexts.org/Bookshel..._(Fiore)/11:_Active_Filters/11.04:_Section_4-

 

[arhzz]

* OK - I see: You have calculated the normalized quantity Ω
* And HOW did you calculate ? Which definition did you apply?

Okay since Tmax is 1/2 I've used this definiton $|T(\Omega )| = \frac{Tmax}{\sqrt{2}}$ Now my Tmax is 1/2 plug in;

$T(\Omega ) = \sqrt{\frac{1+\Omega ^2}{2+200\Omega^2}} = \frac{1}{2\sqrt{2} }$

And solve for omega gives us the solution.

 

[Baluncore]

Ok partially understood except from the "change the order of your circuit from n=2 to n=3".

Each delay element in a filter increases the order by one. A delay element is, each capacitor or inductor in an analogue filter, or each Z^-1 delay in a digital filter. As more delay elements are included, the slope of the transfer function increases. The maximum slope is achieved by optimising the application of the delay elements.

In this example, the inductor initially had no effect on the filter. When an output impedance was realized, the order rose from 2 to 3, as the inductor became an effective part of the filter.

 

[DaveE]

What does L do in the case we connect an output device to this filter so that current flows through L?

Correct me if I'm wrong, but the OP didn't specify any load on this circuit.

L is irrelevant since no current is flowing there ( the circuit is open)

So L is irrelevant, as is your question about what would happen if there was a load. What if the load was a capacitor? Another inductor? A capacitor and an inductor with a shunt resistor?

Just answer the OP's question, don't make it unnecessarily complicated unless they ask you too. The potential complexity is unlimited. You don't get extra points for confusing students. I doubt that he was asking for an online quiz about what the question could have been. If I'm wrong he can ask another question.

 

[Baluncore]

Correct me if I'm wrong, but the OP didn't specify any load on this circuit.

The OP assumed that the load impedance was infinite. But normal practice, and the presence of the inductor, indicate that a finite load impedance should have been specified.

The OP will not be the only reader of this thread, so we need to make the alternative interpretation clear. After all, if the OP was to be the only reader, then we would ask them to delete the thread once they were happy with the answers. We do not want to confuse the future readers.

 

[DaveE]

We do not want to confuse the future readers.

IMO, it is more confusing for future readers to change the problem at hand. New problem → new thread. Although once the discussion about the loaded version of the circuit has been started, it may be reasonable to clear up confusion by discussing the additional poles etc.

If the OP is confused about a 2nd order filter, don't turn it into a 3rd order filter problem. Other readers can ask their questions, perhaps in another thread.

 

[Baluncore]

Although once the discussion about the loaded version of the circuit has been started, it may be reasonable to clear up confusion by discussing the additional poles etc.

That is exactly what we were doing.

Including this unnecessary discussion about how best to help a member, is not helpful when included in the original question thread. Learn from other's mistakes, and try to avoid telling other respondents what they must, or must not, do.