Is it possible to have a plus/minus function that has range of roots?

[Zashmar]

Okay,
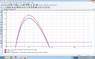
So I have attached a screenshot of my two graphs of a particle shot from a cannon. The blue one has had an air resistance constant of 0.1 applied to it and, as you can see, has 'shrunk'. For the particular question I am investigating a range of answers are plausible ( ie the x-intercepts of the function can vary say \pm 2 units. I have a limited knowledge of parabolas and graphing, so I was thinking maybe some of you guys would be able to tell me if it is possible to have a function that encompasses a set range of x-intercepts and if so, how would i apply this 'method' to a fourth degree polynomial?

I hope you can all see the image I have attached,

Thank you

[/https://www.physicsforums.com/attachment.php?attachmentid=68757&stc=1&d=1397801153b]

 

[SteamKing]

I have a limited knowledge of parabolas and graphing, so I was thinking maybe some of you guys would be able to tell me if it is possible to have a function that encompasses a set range of x-intercepts and if so, how would i apply this 'method' to a fourth degree polynomial?

It's not clear what you mean here.

If you have a fourth-degree polynomial with x-intercepts x1, x2, x3, and x4, then

y = (x-x1)(x-x2)(x-x3)(x-x4)

However, not all fourth degree polynomials will have four x-intercepts. Some will have only two, the other two being complex conjugates, and some will have none, all solutions being complex.

 

[Zashmar]

No I don't mean it like that, I mean if I wanted to define a set of polynomials that had x intercepts between say 38 and 42 on the x axis. In the my particular question i am trying to find a set of polynomials that the particle would land on a 4m^2 square trampoline on the 2d plane,

 

[SteamKing]

No I don't mean it like that, I mean if I wanted to define a set of polynomials that had x intercepts between say 38 and 42 on the x axis. In the my particular question i am trying to find a set of polynomials that the particle would land on a 4m^2 square trampoline on the 2d plane,

Your approach is still obscure.

If you are trying to fire a cannon such that the projectile lands on a certain target, constructing arbitrary polynomials is not the preferred method of solution.

The projectile obeys certain physical laws which describe the path of its flight. The range of a projectile is controlled by two quantities: the angle of elevation above the horizontal and the initial velocity at which the projectile is fired. Various other factors, such as the location of the cannon relative to the target, a difference in elevation, the effect of drag, etc., can also influence the range to certain degrees, if present, and the influence of these other factors may not be represented by simple polynomials.

 

[haruspex]

No I don't mean it like that, I mean if I wanted to define a set of polynomials that had x intercepts between say 38 and 42 on the x axis. In the my particular question i am trying to find a set of polynomials that the particle would land on a 4m^2 square trampoline on the 2d plane,

Yes, parametrically. E.g. If we take quadratics through the origin and through points in the range [a, b] then choose y = Ax(t-x) where t is in [a, b]. Is that what you're after?