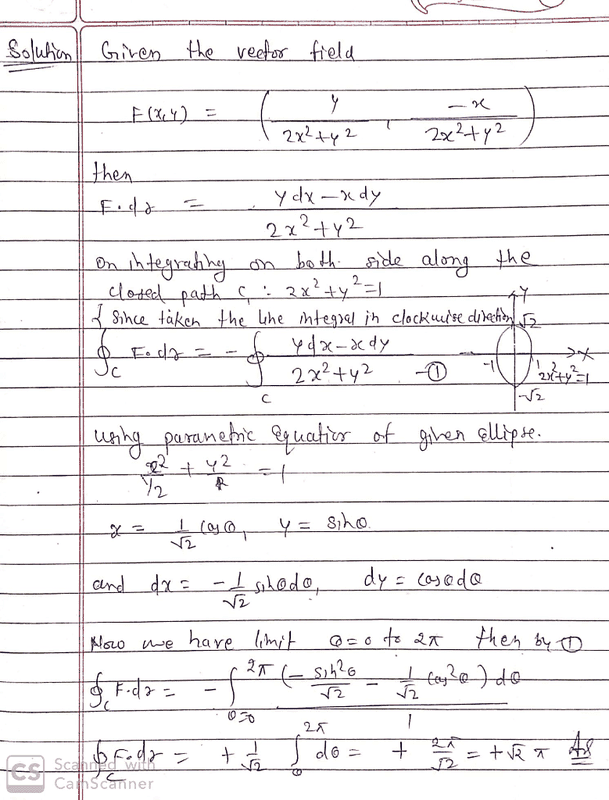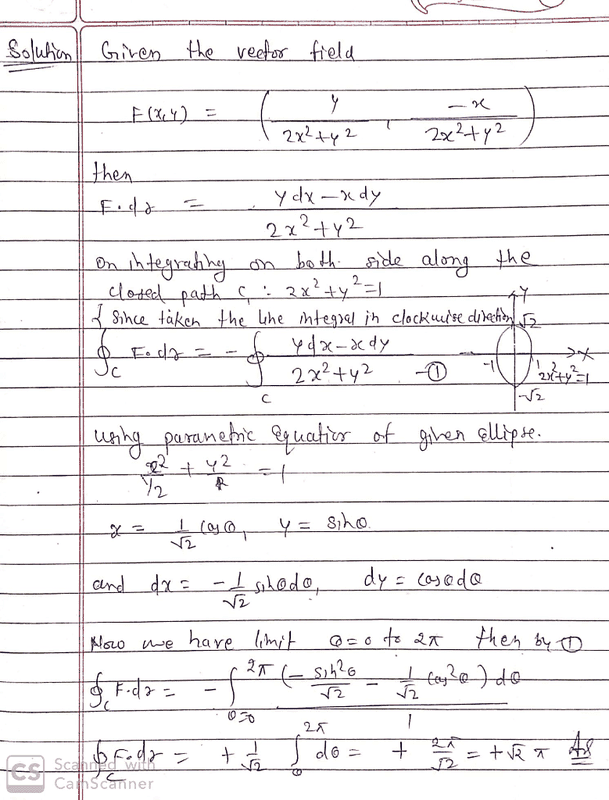Is that field conservative? If yes, why is the work not null?

[Amaelle]

Homework Statement

calculate the closed path integral of the vector field
F(x,y)=(y/(2x^2+y^2) ; -x/(2x^2+y^2)) along the ellipse of equation
{(x, y) ∈ R2: 2x^2 + y^2 = 1} run in clockwise direction

Relevant Equations

x=cos(theta) /sqrt(2)
y=sin(theta)

my problem is the following: this vector field is conservative ( i checked the partial derivative) means the work around a closed path must be zero!√but still the solution says otherwise: any hints?

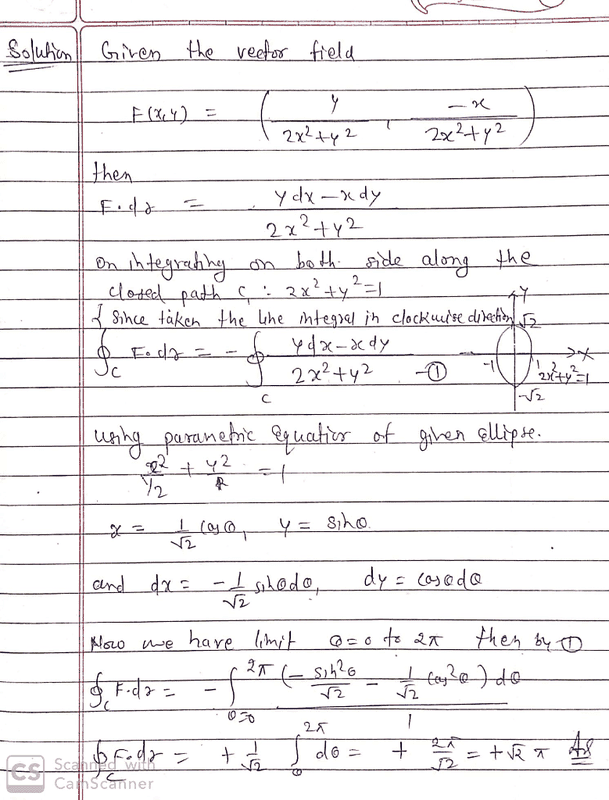explanation? thanks a lot!

 

[pasmith]

Is your vector field defined everywhere inside the ellipse?

 

[Amaelle]

yes I guess

 

[pasmith]

So what is F(0,0)?

 

[Amaelle]

Yes you are right it's not defined there, does this mean that this field is not conservative?

 

[Amaelle]

Do we need continuity condition to assume conservative field?

 

[vela]

Stokes' theorem guarantees the path integral around a closed loop is 0 if the curl vanishes everywhere in region bounded by the loop. In this case, the curl doesn't vanish everywhere inside the loop because the field isn't defined at the origin. There's no guarantee, therefore, that the path integral is 0.

 

[Amaelle]

Thanks a lot for your precious answer, and for the divergence theorem (gauss theorem) do we need to check the same condition to apply it? (the field must be defined everywhere)?

 

[vela]

When I have questions like this, I look up a precise statement of the theorem, something a mathematician would write, because it will state all the conditions that must be satisfied. My calculus book, for example, says the components of the vector field need to be continuously differentiable. Consequently, if there's a singularity in the region of interest, you shouldn't expect to be able to use the theorem.