Is the eccentricity of the lunar orbit constant?

In summary, the Wikipedia article on Lunar distance discusses the confusing graph which suggests that the eccentricity of the lunar orbit is maximal in January and ~July, and minimal in April and ~October. The discussion also addresses the question of whether the eccentricity should be constant, with the conclusion that it varies between 0.044 and 0.067 due to the tidal force of the sun on the earth-moon system. This results in the ellipse rotating once every 8.8479 years, causing the graph to look different each year. Additionally, it is mentioned that the Kepler potential is only an exact solution for the elliptical orbit and the addition of lower order effects, such as tidal forces, breaks this solution.
  • #1
Orthoceras
117
43
TL;DR Summary
Confusion about a graph in wikipedia
The wikipedia article on Lunar distance contains a confusing graph. The graph seems to suggest that the eccentricity of the lunar orbit is maximal in january and ~july, and minimal in april and ~october. I think the eccentricity should be constant. Is wikipedia right or wrong, or is there some trivial confusion?

Moon-Earth_distance,_Moon_phases.gif

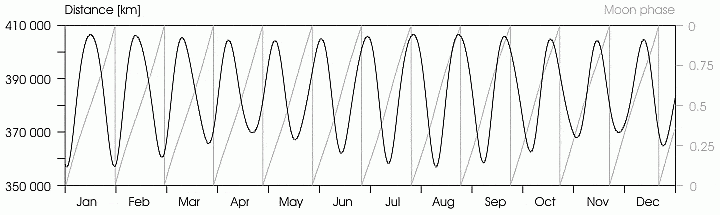
Wikipedia legends: The Moon's distance from the Earth in 2014 ...
 
Last edited:
Astronomy news on Phys.org
  • #2
Orthoceras said:
I think the eccentricity should be constant.
No, the eccentricity varies between 0.044 and 0.067 during the course of half a year; the value e = 0.0549 is just an average. The cause is the tidal force of the sun on the earth-moon system. When the direction to the sun is aligned with the major axis, the eccentricity is biggest, and smallest when aligned with the minor axis. Since the ellipse is not fixed in space, but rotates once every 8.8479 years, the confusing graph will look different from year to year.
 
  • Like
  • Informative
Likes FactChecker, Orthoceras, Orodruin and 1 other person
  • #3
To build upon that: The elliptical orbit of the Kepler potential is only an exact solution for the Kepler potential. Add any lower order effects (such as the tidal forces from the Sun mentioned above) and you will break that. The only question is by how much.
 

1. What is the eccentricity of the lunar orbit?

The eccentricity of the lunar orbit refers to the shape of the orbit of the Moon around the Earth. It is a measure of how elliptical or circular the orbit is, with a value of 0 representing a perfectly circular orbit and a value of 1 representing a highly elliptical orbit.

2. Is the eccentricity of the lunar orbit constant?

No, the eccentricity of the lunar orbit is not constant. It varies over time due to gravitational interactions with other celestial bodies, such as the Sun and the planets. It also changes due to the influence of Earth's tides on the Moon's orbit.

3. How does the eccentricity of the lunar orbit affect the Moon's position in the sky?

The eccentricity of the lunar orbit affects the Moon's position in the sky by causing its distance from Earth to vary. When the eccentricity is higher, the Moon's distance from Earth is greater, resulting in a smaller apparent size in the sky. When the eccentricity is lower, the Moon's distance from Earth is closer, resulting in a larger apparent size in the sky.

4. Can the eccentricity of the lunar orbit be measured?

Yes, the eccentricity of the lunar orbit can be measured using telescopes and mathematical calculations. Scientists can track the Moon's position in the sky over time and use this data to determine the eccentricity of its orbit. This information is important for understanding the Moon's motion and predicting its future positions.

5. How does the eccentricity of the lunar orbit affect lunar eclipses?

The eccentricity of the lunar orbit plays a role in lunar eclipses. When the Moon's orbit is more elliptical, it can be positioned farther away from Earth during a full moon, making it appear smaller and resulting in a partial lunar eclipse. When the Moon's orbit is more circular, it is closer to Earth during a full moon, making it appear larger and resulting in a total lunar eclipse.

Similar threads

I Exploring Gravitational Waves with Earth-Lunar Orbital Perturbations
    • Astronomy and Astrophysics
Replies
1
Views
758
How do tides vary over a lunar cycle?
    • Introductory Physics Homework Help
2
Replies
40
Views
1K
B The Sun's Influence on the Moon's Orbit: Is it Negligible?
    • Classical Physics
Replies
4
Views
740
A What is the cause of lunar nodal and apsidal precession?
    • Astronomy and Astrophysics
2
Replies
36
Views
15K
I Tidal effects on Earth's rotation and moon's orbit
    • Astronomy and Astrophysics
Replies
10
Views
2K
Phases of the Moon: Amateur Questions Answered
    • Astronomy and Astrophysics
Replies
6
Views
3K
Calculating albedo and eccentricity
    • Astronomy and Astrophysics
Replies
3
Views
2K
Writing: Input Wanted Lunar Orbital Rings: Calculating Height and Rotation for Earth-like Gravity
    • Sci-Fi Writing and World Building
Replies
18
Views
3K
Could women be better suited for long distance space travel?
    • Astronomy and Astrophysics
2
Replies
48
Views
12K
A Puzzle Involving the Moon's Orbital Motion
    • Mechanics
Replies
19
Views
1K

Hot Threads

Recent Insights

Back
Top