needingtoknow said:
Is the propagation of a wave simple harmonic motion?
Simple harmonic motion is defined when the restoring force is proportional to the displacement. Hooke's Law F = -kx is an example. However at my level of understanding I have not yet read about the relationship between forces and waves and was just curious if the restoring force is proportional to the displacement when it comes to the propagation of a wave?
The propagation of a wave is
modeled by SHM (Simple Harmonic Motion)
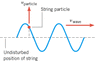
The thumbnail I have attached represents the configuration of a wave propagating on a string. We take a tiny length element (or particle) of the string and model it's
vertical motion as that of SHM. When we do this, we end up with
y(x,t) = Asin(kx - ωt)
Here, y (the vertical position of a particle on the string) is determined by x and t. The amplitude, A, of the waves is usually fixed for this elementary case. The wave speed is determined by
v = k/ω
where k is the wave number and ω is the angular frequency. The wave number, k, is defined as
k = 2π/λ
and the angular frequency, ω, is defined as
ω = 2πf
Thus,
v = λf
where λ is the wavelength between waves on the string and f is the frequency of the wave motion.
Let's consider a "snapshot" of the string (sort of like the picture I have attached) such that t = 0. Then,
y(x,0) = Asin(kx)
Here, we can see that as we increase or decrease our x value, the vertical position of particles on the string varies periodically such as that of SHM.
So, in general, we can model the vertical positions of particles on a string as a function of x and t (that is, space and time). This is a very simplified elementary case though and it only accounts for wave propagation in one spatial dimension. I have also demonstrated a case for which ø = 0 (phase constant) for the sake of simplicity. The phase constant is something you should take more seriously once you start reading more about wave propagation, but hopefully I have helped relate SHM and wave propagation for you on an elementary basis.