Is the Result of the Path Integral Positive Due to Negative dx?

[Ark236]

Homework Statement

Hi everyone.

I was studying an example of Kleppner's book and I have a question.

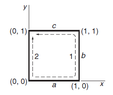
In this example, the path integral is calculated, starting from the point (0,0) and going to the point (0,1). The force is $$F = A(xy \hat{i}+ y^2 \hat{j})$$. The path followed is denoted by (a,b,c) (see figure).

Relevant Equations

$$W = \vec{F}\cdot \vec{dr}$$

In the book it is mentioned that, in path c, the line integral would be:

$$\int \vec{F}\cdot \vec{dr} = A \int_{1}^{0}xy dx = A\int_1^0 x dx = -\dfrac{A}{2}$$.

but I think that dx is negative in that case, the result would be positive, right?

 

[Delta2]

Exactly because dx is negative (because the lower limit of integration is bigger than the higher limit of integration, for this look up the definition of integral as the limit of Riemann Sum) the result would be negative (if A is taken positive).
In order to be more accurate in what is exactly happening, when we take the dot product of $\vec{F}$ and $d\vec{r}$ those two are in opposite directions :$\vec{F}$ points (we can neglect the $\hat j$ component since we take the dot product with path c which is perpendicular to j) in the direction of $\hat i$ since $Axy$ is positive on path c , and $\vec{dr}=dx\hat i$ but dx is negative on path c, so $\vec{dr}$ points in opposite direction to $\hat i$.

Since they point in opposite directions, the dot product is negative.

 

[Orodruin]

To add to that, $dx$ is negative in that integral already because you are integrating from 1 to 0.

 

[Ark236]

Thanks for the answers. It is clear to me that the integral must be negative since the force is opposite to the displacement.

However, the path integral is defined as

$$ W = \int_{a}^{b} \vec{F}\cdot d\vec{r} $$

where a and b refer to the start and end points, respectively.

In this example a = 1 and b = 0, $dr = -dx \hat{i}$. So:

$$ W = \int_{1}^{0} \vec{F}\cdot d\vec{r} =\int_{1}^{0} (xy \hat{i} +y^2\hat{j })\cdot (-dx \hat{i}) = -\int_{1}^{0} xy dx $$

The results, in that case, is positive. According to your answers, my error is that the sign of dx is contain in the integration limit. In that case, I need to consider a positive dx.

 

[Delta2]

No I disagree, it is always $\vec{dr}=dx \hat i +dy \hat j +dz\hat k$, it is that dx , dy, dz can be negative or positive (or zero) depending on the path direction.

 

[Ark236]

So how would you set up the integral of this path?,

$$ W = \int_{1}^{0} \vec{F}\cdot d\vec{r} =\int_{1}^{0} (xy \hat{i} +y^2\hat{j })\cdot (dx \hat{i}) = \int_{1}^{0} xy dx $$

For me it is not totally clear yet the reason.

 

[Delta2]

So how would you set up the integral of this path?,

$$ W = \int_{1}^{0} \vec{F}\cdot d\vec{r} =\int_{1}^{0} (xy \hat{i} +y^2\hat{j })\cdot (dx \hat{i}) = \int_{1}^{0} xy dx $$

For me it is not totally clear yet the reason.

What is not clear? Now you doing it correctly, you just have to put y=1 cause y remains constant and equal to 1 in path c.

 

[Ark236]

Because from the definition, the integration limits are the initial and the final points. From path c the particle starts from the point (0,1) and ends at the point(1,0). Also, the $\vec{dr}$ is the direction of the displacement, in that case, would be negative ($\vec{dr} = -dx \hat{i}$).

 

[vela]

Because from the definition, the integration limits are the initial and the final points. Also, the $\vec{dr}$ is the direction of the displacement, in that case, would be negative ($\vec{dr} = -dx \hat{i}$).

It should be $d\vec{r} = -\lvert dx \rvert\,\hat i$. If you want to put the minus sign in explicitly, you have to use the absolute value of $dx$ to ensure you're using its magnitude.

 

[Delta2]

Because from the definition, the integration limits are the initial and the final points. From path c the particle starts from the point (0,1) and ends at the point(1,0). Also, the $\vec{dr}$ is the direction of the displacement, in that case, would be negative ($\vec{dr} = -dx \hat{i}$).

I don't know why you insist on this, the vector calculus book I 've read (ok its a Greek book written by Greek authors and unknown to the many), defines $d\vec{r}=dx\hat i +...$ and this definition holds regardless of what is the path. It is that depending on path the dx,dy,dz,..., can become negative or positive or zero. In path c it is dy=0 and dx=negative.

 

[Ark236]

Thanks so much for the answer. Now for me is clear :D .