- #1
sudera
- 25
- 0
- Homework Statement
- Find the electric field of a line of charge on the x-axis, with charge density ##\lambda_1## (negative) between ##x=-a## and ##x=0## and charge density ##\lambda_2## (positive) between ##x=0## and ##x = b##.
- Relevant Equations
- ##\dfrac{dE}{dx} = \dfrac{\lambda}{\epsilon_0}##
This is not really homework, but I'm having trouble understanding it intuitively. I came across this when learning about the space charge layer of a diode. The solution I know simply uses the 1D form of Gauss's law: ##\vec{\nabla} \cdot \vec{E}## = ##\dfrac{\rho}{\epsilon_0}## becomes ##\dfrac{dE}{dx} = \dfrac{\lambda}{\epsilon_0}##.
The integral of the left part is an integral of a negative constant, thus will give a declining line. The integral from 0 to the right will give an inclining line (picture below). The electric field is negative everywhere, thus points to the left everywhere. This means that when you placed a positive charge anywhere between ##-a## and ##b##, it would accelerate to the left. But my actual questions is this: what if you place it at ##x=b-\epsilon##, where ##\epsilon## is a small number? It's much closer to all the positive charges than it is to the negative ones so why doesn't it get repelled to the right?
Thanks in advance.
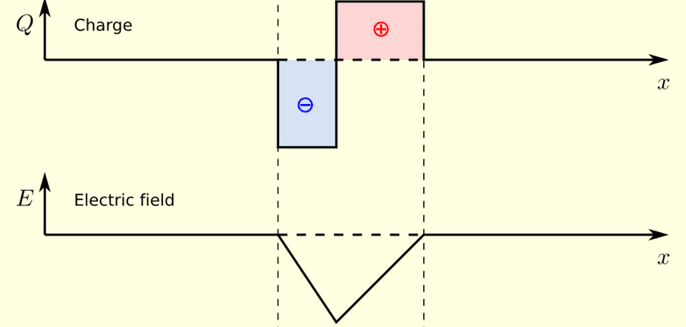
The integral of the left part is an integral of a negative constant, thus will give a declining line. The integral from 0 to the right will give an inclining line (picture below). The electric field is negative everywhere, thus points to the left everywhere. This means that when you placed a positive charge anywhere between ##-a## and ##b##, it would accelerate to the left. But my actual questions is this: what if you place it at ##x=b-\epsilon##, where ##\epsilon## is a small number? It's much closer to all the positive charges than it is to the negative ones so why doesn't it get repelled to the right?
Thanks in advance.