Is there an analytical solution to this equation?

[MigMRF]

So I've derived the rocket equation in empty space and with constant gravity. Now I am interested in adding air resistance. I'm aware that there are 2 different models as if 0<Re<1 then F_drag=k*v and if 1000<Re<30000 then F_drag=1/2*A*rho*CD*v^2. And for my purpose the second model is most fitting (my Re is around 15000. So I've come up with a differentialequation and was wondering if there actually is a solution. Here is my equation:

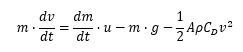
So first of all, is the equation correct. I'm kind of new to differential equations.
And if it's correct then is there an analytical solution.

I'd like some help on this one :D

 

[hilbert2]

There's no closed form solution for that equation unless you find a way to set the mass loss rate, exhaust velocity and air resistance parameters just right to "accidentally" make this have a simple solution.

You can test this by putting some simplified equations of the same type, e.g.

$\displaystyle (1-at)\frac{d^2 x}{dt^2} =b-\left(\frac{dx}{dt}\right)^2$

to Wolfram Alpha for it to try to solve them.