Is There an Easier Method for Solving Truss Problems?

  • Thread starter Thread starter yecko
  • Start date Start date
  • Tags Tags
    Section
Click For Summary
The discussion centers on the challenges of solving truss problems using the method of sections, particularly under time constraints during exams. The original poster expresses concern about the complexity of calculations involving lengths and slopes, seeking simpler methods for solving these problems. A response highlights a potential oversight in the original calculations, specifically the omission of an applied load in the force summation. The conversation emphasizes the need for efficient techniques to handle truss problems effectively within limited time. Overall, participants are exploring ways to simplify the problem-solving process for truss analysis.
yecko
Gold Member
Messages
275
Reaction score
15

Homework Statement


7F9F38F7-E1D4-4C7F-A665-4377358C4063.jpeg


Homework Equations


Method of section

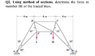
The Attempt at a Solution


This pic below is my attempt, almost solved out length of all the truss... (and i am not sure if my numbers are correct as well for such a troublesome method in solving... )

as my exam would only leave me 15 minutes for each question, so it would be unlikely that i could solve it out with the same method during exam... i am sure there would be simpler ways to solve it...

can anyone suggest any better method to attempt the question?
Thank you very much!

FC77E2DF-BBFF-45E3-9238-81F4FACA6F4F.jpeg
 

Attachments

  • FC77E2DF-BBFF-45E3-9238-81F4FACA6F4F.jpeg
    FC77E2DF-BBFF-45E3-9238-81F4FACA6F4F.jpeg
    53.6 KB · Views: 448
  • 7F9F38F7-E1D4-4C7F-A665-4377358C4063.jpeg
    7F9F38F7-E1D4-4C7F-A665-4377358C4063.jpeg
    17.7 KB · Views: 949
Last edited:
Physics news on Phys.org
It is a bit of a pain to calculate lengths and slopes using geometry and trig. I'm not sure where yourverrir might be in the geometry, if any, but when you summed forces in the y direction, you forgot to include the applied load L.
 
Last edited:

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?
View full post »

Similar threads

Find the Period of Oscillation for a Mass Falling Through a Tunnel Through the Earth
  • · Replies 7 ·
Replies
7
Views
1K
Help understanding how to determine Compress or Tension in Truss
  • · Replies 3 ·
Replies
3
Views
7K
Statics: Statically Indeterminate Unstable Plane Truss
  • · Replies 4 ·
Replies
4
Views
5K
Is it possible to solve relative velocity problems without sine law?
  • · Replies 25 ·
Replies
25
Views
2K
Finding Forces in Truss Members Using Method of Sections
  • · Replies 3 ·
Replies
3
Views
2K
Solving this problem using the energy method
  • · Replies 7 ·
Replies
7
Views
2K
What is the eccentricity of an orbit such that Vp = 2Va?
  • · Replies 5 ·
Replies
5
Views
1K
When can using a logarithm make solving an equation easier?
  • · Replies 2 ·
Replies
2
Views
2K
Methods of Section: Truss problem
  • · Replies 4 ·
Replies
4
Views
1K
Can You Solve Graphical Vector Problems Using Only Math and Integration?
  • · Replies 2 ·
Replies
2
Views
1K