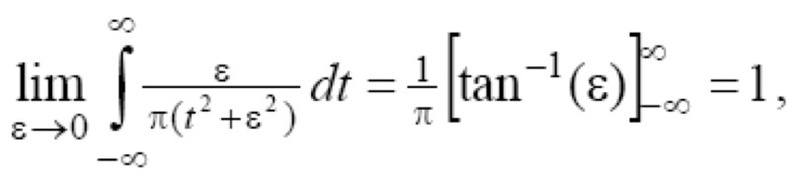Discussion Overview
The discussion revolves around the equivalent forms of the arctangent function, particularly in the context of an integral representation. Participants explore various mathematical manipulations and substitutions related to the arctan function, specifically addressing the role of the variable epsilon (ε) in these expressions.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant mentions a formula for arctan as an integral, specifically arctan(x) = ∫(dt)/(a²+t²), and seeks clarification on its correctness.
- Another participant provides a link to an article that contains various forms of inverse trigonometric functions, including arctan.
- Some participants express concern that the use of ε in the context of arctan may be misleading and propose substituting variables to clarify the integral.
- There is a suggestion to manipulate the integral to achieve a standard form, specifically ∫(1/(1+x²)) dx, by factoring out ε² from the denominator.
- Participants discuss the implications of substituting u := t/ε and how it affects the argument of arctan, questioning how ε relates to the limits of the function.
- One participant notes that the notation involving ε is confusing but considers it a temporary result, indicating a lack of consensus on its appropriateness.
- There is a discussion about the correctness of the final result being 1, while some participants find the presence of ε in the calculations odd or potentially erroneous.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the appropriateness of using ε in the context of arctan, with some finding it misleading while others focus on the correctness of the final result. The discussion remains unresolved regarding the clarity and correctness of the integral manipulations.
Contextual Notes
There are unresolved questions regarding the assumptions made about the variable ε and its role in the integral representation of arctan. The discussion also highlights potential ambiguities in notation and variable substitution.