Is this manipulation "evil" or simply not intuitive due to unfamiliarity?

[JC2000]

Homework Statement

Show that :
$$
\beta(p, q)=\int_{0}^{\infty} \frac{y^{q-1}}{(1+y)^{p+q}} d y
$$

Relevant Equations

The Beta Function :

$$
\beta(m, n)=\int_{0}^{1} x^{m-1}(1-x)^{n-1} d x
$$

The solution is as follows :

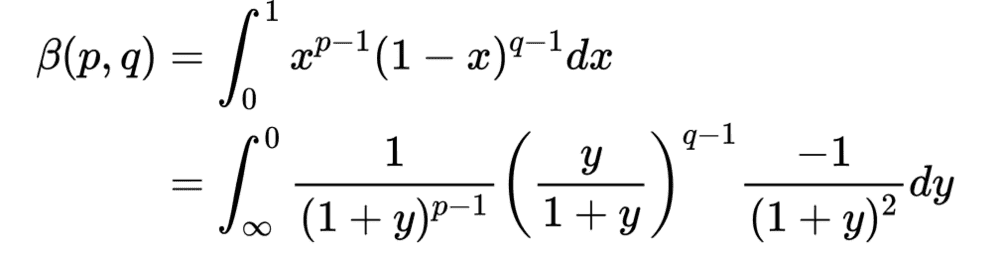
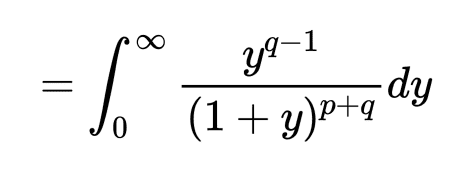The substitution is what nags me , which is as follows :

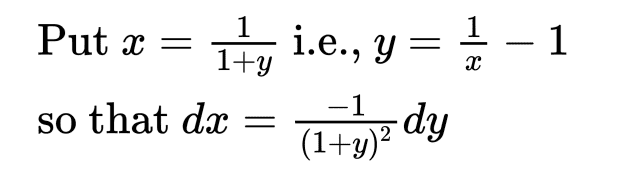
This substitution "trick" to me seems impossibly difficult to arrive at "logically" without pretty much reverse engineering the problem.
So is this simply a lack of practice/ familiarisation showing ? I feel like I have always struggled with similar manipulations. In the past I think it was through repeatedly encountering a certain peculiar manipulation that it would become second nature for me. Is this how such problems are to be approached? Since it seems to almost be the same as memorising the solution!

Thank you for your insight!

 

[pbuk]

Substitutions for indefinite integrals can be tricky and you pretty much have to learn them, however for definite integrals the question gives you a big clue - look at the limits.

 

[JC2000]

Substitutions for indefinite integrals can be tricky and you pretty much have to learn them, however for definite integrals the question gives you a big clue - look at the limits.

For indefinite integrals do you mean I should start listing the substitutions once they ambush me or is it fine to internalise them by practicing often?

So for this integral since the beta function has limits 0 and 1 while the question has limits 0 and infinity, I must search for a substitution whereby the desired transformation of limits is achieved (?)

Thanks for the input!

 

[pbuk]

For indefinite integrals do you mean I should start listing the substitutions once they ambush me or is it fine to internalise them by practicing often?

Practice, practice, practice

So for this integral since the beta function has limits 0 and 1 while the question has limits 0 and infinity, I must search for a substitution whereby the desired transformation of limits is achieved (?)

Yes - if you see $\infty$ on one side of the transformation you know you are looking for a substitution where one limit goes to 1/0, if you see $\pi$ on one side only you are looking for a trigonometric substitution etc. Don't forget to consider (as in this case) that the transformation might 'swap' the upper and lower limit.

 

[benorin]

This tip is on pg. 76 of Special Functions by Askey, Andrews, and Roy in the chapter on hypergeometric functions:

There are six linear fractional transformations that will map a set of three points to a permutation of the three points. For example, the set $\left\{ 0,1,\infty\right\}$ will be mapped to itself by the mappings

$$x\rightarrow \, x, \, 1-x, \, \tfrac{1}{x} , \, \tfrac{1}{1-x} , \, 1-\tfrac{1}{x} = \tfrac{x-1}{x} , \, \tfrac{1}{1-\tfrac{1}{x}} = \tfrac{x}{x-1}$$