Is This Surface Integral Correct?

[Apashanka]

Homework Statement

Requesting for re check

Relevant Equations

Requesting for re check

Problem Statement: Requesting for re check
Relevant Equations: Requesting for re check

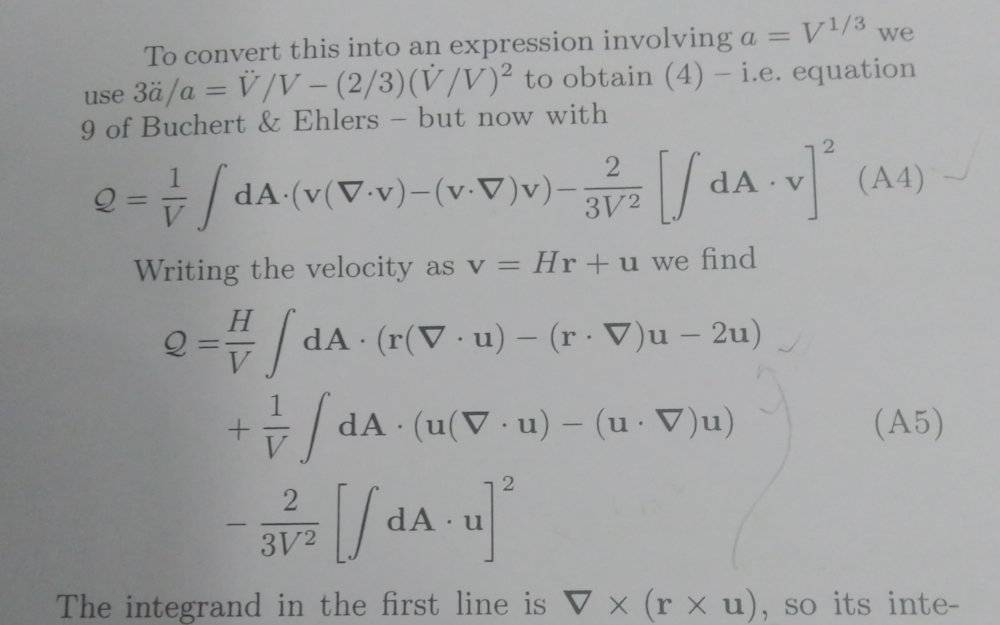
In this eq.A4 putting $v=Hr+u$ the first integrand in eq.A5 is coming as $H(r(\nabla•u)-(r•\nabla)u+2u)\ne\nabla×(r×u)$
Am I right??
Can I request anyone to please recheck it...
using this the author has put the term $\int_s(da•\nabla×(r×u))=0$(as closed surface) how then it is coming??
Will anyone please help...
$r$ is the position vector and $u$ is the peculiar velocity

 

[TSny]

In this eq.A4 putting $v=Hr+u$ the first integrand in eq.A5 is coming as $H(r(\nabla•u)-(r•\nabla)u+2u)\ne\nabla×(r×u)$
Am I right??

Shouldn't the last term on the left be $-2u$ instead of $+2u$?

I'm not sure of the full meaning and context of the symbols. However, as a vector identity, I believe it is true that
$${\bf r} (\nabla \cdot {\bf u})-({\bf r} \cdot \nabla) {\bf u} -2 {\bf u}=\nabla×({\bf r} × {\bf u})$$

 

[Apashanka]

Shouldn't the last term on the left be $-2u$ instead of $+2u$?

I'm not sure of the full meaning and context of the symbols. However, as a vector identity, I believe it is true that
$$r(\nabla•u)-(r•\nabla)u-2u=\nabla×(r×u)$$

Sir the last term is coming as $2u$ instead of $-2u$ e.g putting $v=Hr+u$ in eqA4 we get $v(\nabla•v)=(Hr+u)(3H+\nabla•u)=3H^2r+Hr(\nabla•u)+3Hu+u(\nabla•u)$
Similarly $-(v•\nabla)v=-[(Hr+u)•\nabla](Hr+u)=-(H^2r+H(r•\nabla)u+Hu+(u•\nabla)u)$
Similarly $-\frac{2}{3V^2}[\int_s(da•v)]^2=-\frac{2}{3V^2}[\int_s(da•Hr)]^2-\frac{2}{3V^2}[\int(da•u)]^2=-6H^2-\frac{2}{3V^2}[\int(da•u)]^2$
Now adding these terms of the integrand we rest all term same except $2Hu$ instead of $-2Hu$ for which the author has simplified this to $\nabla×(r×u)$ and put it's surface integral to 0 (assuming closed surface) which is not coming true here...
That's what I want to clarify

 

[TSny]

Similarly $-\frac{2}{3V^2}[\int_s(da•v)]^2=-\frac{2}{3V^2}[\int_s(da•Hr)]^2-\frac{2}{3V^2}[\int(da•u)]^2$

There is a third term that should be included on the right side. Including this missing term should make everything OK.

 

[Apashanka]

There is a third term that should be included on the right side. Including this missing term should make everything OK.

Sorry I didn't get you

 

[Apashanka]

Sorry I didn't get you

Oh yes sir got it ...silly mistake
...thanks