bio
- 12
- 0
Jack draws rings of rhombuses about a common centre point. All rhombuses have the same side length.
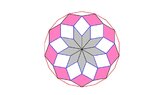
Rhombuses in the first, or inner, ring are all identical. Each rhombus has a vertex at the centre and each of its sides that meet at the centre is shared with another rhombus. They all have the same size angle at the centre. Figure 1 shows a first ring with 7 rhombuses.
Each rhombus in the second ring has two adjacent sides each of which is shared with a rhombus in the first ring. Figure 2 shows the second ring when the first ring contains 7 rhombuses.
Jack continues adding rings of rhombuses in the same way for as long as possible. Figure 3 shows the third ring when the first ring contains 7 rhombuses. In this example, since it is not possible to draw any new rhombuses that share an edge with two rhombuses in the third ring, there are only three rings in this rhombus ring pattern.
a) In another rhombus ring pattern, each rhombus in the last ring has an angle of 20 degrees and each rhombus in the second last ring has an angle of 60 degrees. How many rhombuses are in each ring, and how many rings are there in this rhombus ring pattern?
Figures 1, 2 and 3 can be found at this link. https://imgur.com/a/qN4yDVe
Rhombuses in the first, or inner, ring are all identical. Each rhombus has a vertex at the centre and each of its sides that meet at the centre is shared with another rhombus. They all have the same size angle at the centre. Figure 1 shows a first ring with 7 rhombuses.
Each rhombus in the second ring has two adjacent sides each of which is shared with a rhombus in the first ring. Figure 2 shows the second ring when the first ring contains 7 rhombuses.
Jack continues adding rings of rhombuses in the same way for as long as possible. Figure 3 shows the third ring when the first ring contains 7 rhombuses. In this example, since it is not possible to draw any new rhombuses that share an edge with two rhombuses in the third ring, there are only three rings in this rhombus ring pattern.
a) In another rhombus ring pattern, each rhombus in the last ring has an angle of 20 degrees and each rhombus in the second last ring has an angle of 60 degrees. How many rhombuses are in each ring, and how many rings are there in this rhombus ring pattern?
Figures 1, 2 and 3 can be found at this link. https://imgur.com/a/qN4yDVe