Just looking for confirmation for a torque calculation

[jbriggs444]

I = 1/6 × (m 0.0075 x length 0.01 squared)

= 0.000000125 m2

0.000000125 kg m²

W= pi/ 0.001 =3141.59 radians per second

Agreed. $\omega_\text{avg}$ = 3141.59 radians per second.

Angular acceleration (a) = changing w / changing t

As initial w is zero it easily is 3141.59
/
0.001 seconds = 3,141,590 rads per second

You are going a bit off the rails here.

You have calculated the average rotation rate as 3141.59 radians per second. I agree that you know the initial rotation rate. What you have not calculated yet is the final rotation rate.

You need the final rotation rate so that you can figure out the difference between the final rotation rate and the initial rotation rate.

Alternately, you could figure out the difference between the average rotation rate and the initial rotation rate and then divide by half of the elapsed time since the average rotation rate will be achieved halfway through the interval.

The units are also incorrect. Angular acceleration should be in rads per second per second.

Stopping at the first discovered error.

 

[Steve4Physics]

@pete94857 I’d like to add to what @jbriggs444 has said,. You might want to try this…

A car has mass 1000kg (not ‘weight 1000kg’ by the way, because in physics 'weight' is a gravitational force measured in newtons!).

The car accelerates uniformly from rest and covers a distance of 100m in 10s.

a) What is the car’s initial speed?
b) What is the car’s average speed?
c) What is the car’s final speed?
d) What is the car’s final kinetic energy?

Your original problem isn’t that different from the above if you think about it. You are just using angles rather than distances and moment of inertia rather than mass.

 

[pete94857]

0.000000125 kg m²


Agreed. $\omega_\text{avg}$ = 3141.59 radians per second.


You are going a bit off the rails here.

You have calculated the average rotation rate as 3141.59 radians per second. I agree that you know the initial rotation rate. What you have not calculated yet is the final rotation rate.

You need the final rotation rate so that you can figure out the difference between the final rotation rate and the initial rotation rate.

Alternately, you could figure out the difference between the average rotation rate and the initial rotation rate and then divide by half of the elapsed time since the average rotation rate will be achieved halfway through the interval.

The units are also incorrect. Angular acceleration should be in rads per second per second.

Stopping at the first discovered error.

Isn't the angular velocity the final rotation rate ?

Angular velocity.... w = radians/time

W= pi/ 0.001 =3141.59 radians sec2

If so any function against zero would surely produce the same value. Please explain

Edit ... because it's in 180 degrees, pi radians accounts for it

So now I'm confused

 

[pete94857]

@pete94857 I’d like to add to what @jbriggs444 has said,. You might want to try this…

A car has mass 1000kg (not ‘weight 1000kg’ by the way, because in physics 'weight' is a gravitational force measured in newtons!).

The car accelerates uniformly from rest and covers a distance of 100m in 10s.

a) What is the car’s initial speed?
b) What is the car’s average speed?
c) What is the car’s final speed?
d) What is the car’s final kinetic energy?

Your original problem isn’t that different from the above if you think about it. You are just using angles rather than distances and moment of inertia rather than mass.

I'm trying to do this problem first thank you.

 

[jbriggs444]

Isn't the angular velocity the final rotation rate ?

Which angular velocity are you talking about?

There is the initial angular velocity. That is zero. That is not equal to the final rotation rate.
There is the average angular velocity. That is 3141.59 radians per second. That second is not squared.
There is the final angular velocity. That is something that you have not calculated.

Angular velocity.... w = radians/time

The units for angular velocity are usually radians per time unit, yes. But that does not tell us anything much.

If the angular velocity were constant then one could calculate the one and only angular velocity by dividing the angle rotated through ($\Delta \theta$) by the time elapsed ($\Delta t$).

But the angular velocity here is not constant.

W= pi/ 0.001 =3141.59 radians sec2

That is not correct.

A correct statement would be that $\omega_\text{avg} = \frac{\Delta \theta}{\Delta t} = \frac{\pi \text{ radians}}{0.001 \text{ seconds}}$ = 3141.59 radians/sec

A helpful equation is: $\omega_\text{avg} = \frac{\omega_0 + \omega_f}{2}$. When starting from rest under uniform acceleration, the average rotation rate is half of the final rotation rate.

If so any function against zero would surely produce the same value. Please explain

Explain what?

Edit ... because it's in 180 degrees, pi radians accounts for it

I have no objection to 180 degrees being $\pi$ radians. The difficulty is your confusion between average rotation rate and final rotation rate when the rotation rate is not constant.

So now I'm confused

Yes. We get that.

 

[pete94857]

Which angular velocity are you talking about?

There is the initial angular velocity. That is zero. That is not equal to the final rotation rate.
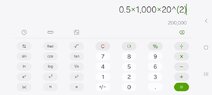
There is the average angular velocity. That is 3141.59 radians per second. That second is not squared.
There is the final angular velocity. That is something that you have not calculated.


The units for angular velocity are usually radians per time unit, yes. But that does not tell us anything much.

If the angular velocity were constant then one could calculate the one and only angular velocity by dividing the angle rotated through ($\Delta \theta$) by the time elapsed ($\Delta t$).

But the angular velocity here is not constant.

Which angular velocity are you talking about?

There is the initial angular velocity. That is zero. That is not equal to the final rotation rate.
There is the average angular velocity. That is 3141.59 radians per second. That second is not squared.
There is the final angular velocity. That is something that you have not calculated.


The units for angular velocity are usually radians per time unit, yes. But that does not tell us anything much.

If the angular velocity were constant then one could calculate the one and only angular velocity by dividing the angle rotated through ($\Delta \theta$) by the time elapsed ($\Delta t$).

But the angular velocity here is not constant.


That is not correct.

A correct statement would be that $\omega_\text{avg} = \frac{\Delta \theta}{\Delta t} = \frac{\pi \text{ radians}}{0.001 \text{ seconds}}$ = 3141.59 radians/sec

A helpful equation is: $\omega_\text{avg} = \frac{\omega_0 + \omega_f}{2}$. When starting from rest under uniform acceleration, the average rotation rate is half of the final rotation rate.


Explain what?


I have no objection to 180 degrees being $\pi$ radians. The difficulty is your confusion between average rotation rate and final rotation rate when the rotation rate is not constant.


Yes. We get that.

That is not correct.

A correct statement would be that $\omega_\text{avg} = \frac{\Delta \theta}{\Delta t} = \frac{\pi \text{ radians}}{0.001 \text{ seconds}}$ = 3141.59 radians/sec

A helpful equation is: $\omega_\text{avg} = \frac{\omega_0 + \omega_f}{2}$. When starting from rest under uniform acceleration, the average rotation rate is half of the final rotation rate.


Explain what?


I have no objection to 180 degrees being $\pi$ radians. The difficulty is your confusion between average rotation rate and final rotation rate when the rotation rate is not constant.


Yes. We get that.

I apologise for missing bits out ref should be pi radians/ time. I'm finding it difficult to see why the angular velocity is not equal to the final velocity.

 

[Steve4Physics]

I'm trying to do this problem first thank you.

You should find your Post #1 problem easier once you can do the (simpler) Post #37 problem!

 

[pete94857]

I apologise for missing bits out ref should be pi radians/ time. I'm finding it difficult to see why the angular velocity is not equal to the final velocity.

OK I get it....

 

[pete94857]

I apologise for missing bits out ref should be pi radians/ time. I'm finding it difficult to see why the angular velocity is not equal to the final velocity.

OK here we go... again...

I have a solid 10 mm cube being rotated around it's own axis the axis is in the centre of a side and goes straight through to the opposite side.
It weights 7.5 grams
No drag or friction.
I want to know how much energy J will be used to accelerate it and complete a 180 degree rotation in 0.001 seconds starting from zero velocity.

I don't have the correct symbols etc on my phone fonts so some parts I'll just have to word.

Part one. Finding inertia I need the length of my cube in metres and the weight in kg. Then multiply them then divide by six.

I = 1/6 × (m 0.0075 x length 0.01 squared)
= 0.000000125 m2

Next bit...

Average Angular velocity.... w = radians/time

W= pi/ 0.001 =3141.59 radians per second squared.

As the average angular velocity is half the final velocity (uniformed acceleration) if it wasn't a uniformed acceleration I'd need to elaborate further. Maybe.

3141.59 x 2 = 6,283.18 radians per second squared.

Next is ...

Angular acceleration (a) = changing w / changing t

As initial w is zero it easily is 6,283.18 / 0.001 seconds = 6,283,180 radians per second squared.

Then ...

Torque T = l x a

0.000000125 x 6,283,180 = 0.7853975 Nm

Last bit ...

Work W = T x pi radians

0.7853975 x pi radians = 2.4673990161 J

 

[pete94857]

OK here we go... again...

I have a solid 10 mm cube being rotated around it's own axis the axis is in the centre of a side and goes straight through to the opposite side.
It weights 7.5 grams
No drag or friction.
I want to know how much energy J will be used to accelerate it and complete a 180 degree rotation in 0.001 seconds starting from zero velocity.

I don't have the correct symbols etc on my phone fonts so some parts I'll just have to word.

Part one. Finding inertia I need the length of my cube in metres and the weight in kg. Then multiply them then divide by six.

I = 1/6 × (m 0.0075 x length 0.01 squared)
= 0.000000125 m2

Next bit...

Average Angular velocity.... w = radians/time

W= pi/ 0.001 =3141.59 radians per second squared.

As the average angular velocity is half the final velocity (uniformed acceleration) if it wasn't a uniformed acceleration I'd need to elaborate further. Maybe.

3141.59 x 2 = 6,283.18 radians per second squared.

Next is ...

Angular acceleration (a) = changing w / changing t

As initial w is zero it easily is 6,283.18 / 0.001 seconds = 6,283,180 radians per second squared.

Then ...

Torque T = l x a

0.000000125 x 6,283,180 = 0.7853975 Nm

Last bit ...

Work W = T x pi radians

0.7853975 x pi radians = 2.4673990161 J

If I were to change the time by a factor of 10 example 0.01 could I simply change the final answer to 0.2467 J, I'm assuming yes as looking through it that seems logical.

 

[jbriggs444]

Part one. Finding inertia I need the length of my cube in metres and the weight in kg. Then multiply them then divide by six.

I = 1/6 × (m 0.0075 x length 0.01 squared)
= 0.000000125 m2

The units are kg m². You are still dropping the kg.

Average Angular velocity.... w = radians/time

W= pi/ 0.001 =3141.59 radians per second squared.

As the average angular velocity is half the final velocity (uniformed acceleration) if it wasn't a uniformed acceleration I'd need to elaborate further. Maybe.

3141.59 x 2 = 6,283.18 radians per second squared.

The units for angular velocity are radians per second. Not radians per second squared.

Yes, if this was not uniform acceleration then things would become more difficult.

Angular acceleration (a) = changing w / changing t

As initial w is zero it easily is 6,283.18 / 0.001 seconds = 6,283,180 radians per second squared.

This time the units are right. Angular acceleration is measured in radians per second squared.

Torque T = l x a

0.000000125 x 6,283,180 = 0.7853975 Nm

If you were keeping track of units, that would be kg m² times radians per second squared giving kg m²/second². Which does indeed turn out to be the same thing as a Newton-meter.

Work W = T x pi radians

0.7853975 x pi radians = 2.4673990161 J

Yes. Radians are dimensionless, and a Joule is another name for a Newton-meter.

It would be good to have a sanity check. Let us take that final rotation rate (6283.18 rad/sec) and use it to compute a final kinetic energy.

$KE = \frac{1}{2}I \omega^2 = 0.5 \times 0.000000125 \times 6283.18^2$ = 2.467 J.

Yes, that checks out. Work in is equal to energy out.

 

[jbriggs444]

If I were to change the time by a factor of 10 example 0.01 could I simply change the final answer to 0.2467 J, I'm assuming yes as looking through it that seems logical.

One always needs to be careful when scaling a problem. Does the answer change linearly with the scale factor? Quadratically? Inverse? Inverse quadratically? Something else? A classic example of this kind of issue is the cube-square problem.

If you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you divide this reduced rotation rate by the increased time, you will see that the required acceleration is reduced by a factor of 100. So the final result is reduced by a factor of 100.

Alternately, if you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you calculate rotational kinetic energy, the result is reduced by a factor of 100 because the $\omega$ is squared in the formula. So again, by this line of reasoning, we get a reduction by a factor of 100.

So in this case the answer scales inverse quadratically with the elapsed time.

 

[pete94857]

One always needs to be careful when scaling a problem. Does the answer change linearly with the scale factor? Quadratically? Inverse? Inverse quadratically? Something else? A classic example of this kind of issue is the cube-square problem.

If you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you divide this reduced rotation rate by the increased time, you will see that the required acceleration is reduced by a factor of 100. So the final result is reduced by a factor of 100.

Alternately, if you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you calculate rotational kinetic energy, the result is reduced by a factor of 100 because the $\omega$ is squared in the formula. So again, by this line of reasoning, we get a reduction by a factor of 100.

So in this case the answer scales quadratically with the elapsed time.

Ah yes I see, thanks very much.

The units are kg m². You are still dropping the kg.


The units for angular velocity are radians per second. Not radians per second squared.

Yes, if this was not uniform acceleration then things would become more difficult.


This time the units are right. Angular acceleration is measured in radians per second squared.


If you were keeping track of units, that would be kg m² times radians per second squared giving kg m²/second². Which does indeed turn out to be the same thing as a Newton-meter.


Yes. Radians are dimensionless, and a Joule is another name for a Newton-meter.

It would be good to have a sanity check. Let us take that final rotation rate (6283.18 rad/sec) and use it to compute a final kinetic energy.

$KE = \frac{1}{2}I \omega^2 = 0.5 \times 0.000000125 \times 6283.18^2$ = 2.467 J.

Yes, that checks out. Work in is equal to energy out.

Thanks

 

[pete94857]

The units are kg m². You are still dropping the kg.


The units for angular velocity are radians per second. Not radians per second squared.

Yes, if this was not uniform acceleration then things would become more difficult.


This time the units are right. Angular acceleration is measured in radians per second squared.


If you were keeping track of units, that would be kg m² times radians per second squared giving kg m²/second². Which does indeed turn out to be the same thing as a Newton-meter.


Yes. Radians are dimensionless, and a Joule is another name for a Newton-meter.

It would be good to have a sanity check. Let us take that final rotation rate (6283.18 rad/sec) and use it to compute a final kinetic energy.

$KE = \frac{1}{2}I \omega^2 = 0.5 \times 0.000000125 \times 6283.18^2$ = 2.467 J.

Yes, that checks out. Work in is equal to energy out.

Got it. you're a star

 

[pete94857]

One always needs to be careful when scaling a problem. Does the answer change linearly with the scale factor? Quadratically? Inverse? Inverse quadratically? Something else? A classic example of this kind of issue is the cube-square problem.

If you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you divide this reduced rotation rate by the increased time, you will see that the required acceleration is reduced by a factor of 100. So the final result is reduced by a factor of 100.

Alternately, if you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you calculate rotational kinetic energy, the result is reduced by a factor of 100 because the $\omega$ is squared in the formula. So again, by this line of reasoning, we get a reduction by a factor of 100.

So in this case the answer scales inverse quadratically with the elapsed time.

All notes made ,thanks again for your patience and time it means a lot to me.

 

[jbriggs444]

There is another less important matter that I did not want to bring up while we were still trying to agree upon a solution.

When working a problem, it is good practice to work with symbols and algebra all the way to the end and only substitute numbers in once one has a finished formula in hand.

It is a hard practice to follow. My own inclination is much like yours. I try to figure out one piece at a time, putting numbers to everything and doing some sanity checks as I go to make sure that I've not fallen off the rails halfway through.

Let us try to work the problem symbolically. I will be thinking and writing as I go, so please forgive any wrong turns along the way.

Our strategy will be the one that you have chosen. Figure the rotation rate. Use that to compute the acceleration rate. Use that to compute torque. And use that to compute rotational work.

The average rotation rate ($\omega_\text{avg}$) is given by the angle rotated through ($\Delta \theta$) divided by the elapsed time ($\Delta t)$:$$\omega_\text{avg} = \frac{\Delta \theta}{\Delta t}$$For constant acceleration, the average rotation rate is also given by:$$\omega_\text{avg} = \frac{\omega_f - \omega_0}{2}$$We can relax our rule about plugging in numbers and simply take $\omega_0$ as 0. It is more of a fixed feature of the problem than an adjustable parameter. We can solve and get:$$\omega_f = \frac{2 \Delta \theta}{\Delta t}$$We know that angular acceleration ($\alpha$) is given by the change in angular velocity divided by the change in time. Or:$$\alpha = \frac{\omega_f - \omega_0}{\Delta t} = \frac{\omega_f}{\Delta t} = \frac{2 \Delta \theta}{{\Delta t}^2}$$We need to convert that angular acceleration to a torque ($\tau$) using:$$\tau = I \alpha$$For a cube with side length $l$ about an axis through the centers of two opposing faces, we have the formula:$$I = \frac{1}{6}ml^2$$Substituting, we get:$$\tau = \frac{1}{6}ml^2 \times \frac{2 \Delta \theta}{{\Delta t}^2} = \frac{ml^2 \Delta \theta}{3 {\Delta t}^2}$$To get work from torque, we need to multiply by the rotation angle ($\Delta \theta$). This gives:$$E = \tau \Delta \theta = \frac{ml^2 {\Delta \theta}^2}{3 {\Delta t}^2}$$Now goodness only knows, I have the ability to screw up the algebra. So let us plug in some numbers.

$m$ = 0.0075 kg
$l$ = 0.01 m
$\Delta \theta$ = 180 degrees = $\pi$ radians = 3.14159 radians
$\Delta t$ = 0.001 seconds.

I get 2.46740 kg m²/sec²

Wowsers. And we can see the inverse quadratic scaling with $\Delta t$ right there in the formula.

 

[pete94857]

One always needs to be careful when scaling a problem. Does the answer change linearly with the scale factor? Quadratically? Inverse? Inverse quadratically? Something else? A classic example of this kind of issue is the cube-square problem.

If you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you divide this reduced rotation rate by the increased time, you will see that the required acceleration is reduced by a factor of 100. So the final result is reduced by a factor of 100.

Alternately, if you increase the time by a factor of 10, you reduce the final rotation rate by a factor of 10. If you calculate rotational kinetic energy, the result is reduced by a factor of 100 because the $\omega$ is squared in the formula. So again, by this line of reasoning, we get a reduction by a factor of 100.

So in this case the answer scales inverse quadratically with the elapsed time.

So increasing the time to 0.01 seconds instead of 0.001 seconds the final energy will be 0.02467 J

 

[pete94857]

There is another less important matter that I did not want to bring up while we were still trying to agree upon a solution.

When working a problem, it is good practice to work with symbols and algebra all the way to the end and only substitute numbers in once one has a finished formula in hand.

It is a hard practice to follow. My own inclination is much like yours. I try to figure out one piece at a time, putting numbers to everything and doing some sanity checks as I go to make sure that I've not fallen off the rails halfway through.

Let us try to work the problem symbolically. I will be thinking and writing as I go, so please forgive any wrong turns along the way.

Our strategy will be the one that you have chosen. Figure the rotation rate. Use that to compute the acceleration rate. Use that to compute torque. And use that to compute rotational work.

The average rotation rate ($\omega_\text{avg}$) is given by the angle rotated through ($\Delta \theta$) divided by the elapsed time ($\Delta t)$:$$\omega_\text{avg} = \frac{\Delta \theta}{\Delta t}$$For constant acceleration, the average rotation rate is also given by:$$\omega_\text{avg} = \frac{\omega_f - \omega_0}{2}$$We can relax our rule about plugging in numbers and simply take $\omega_0$ as 0. It is more of a fixed feature of the problem than an adjustable parameter. We can solve and get:$$\omega_f = \frac{2 \Delta \theta}{\Delta t}$$We know that angular acceleration ($\alpha$) is given by the change in angular velocity divided by the change in time. Or:$$\alpha = \frac{\omega_f - \omega_0}{\Delta t} = \frac{\omega_f}{\Delta t} = \frac{2 \Delta \theta}{{\Delta t}^2}$$We need to convert that angular acceleration to a torque ($\tau$) using:$$\tau = I \alpha$$For a cube with side length $l$ about an axis through the centers of two opposing faces, we have the formula:$$I = \frac{1}{6}ml^2$$Substituting, we get:$$\tau = \frac{1}{6}ml^2 \times \frac{2 \Delta \theta}{{\Delta t}^2} = \frac{ml^2 \Delta \theta}{3 {\Delta t}^2}$$To get work from torque, we need to multiply by the rotation angle ($\Delta \theta$). This gives:$$E = \tau \Delta \theta = \frac{ml^2 {\Delta \theta}^2}{3 {\Delta t}^2}$$Now goodness only knows, I have the ability to screw up the algebra. So let us plug in some numbers.

$m$ = 0.0075 kg
$l$ = 0.01 m
$\Delta \theta$ = 180 degrees = $\pi$ radians = 3.14159 radians
$\Delta t$ = 0.001 seconds.

I get 2.46740 kg m²/sec²

Wowsers. And we can see the inverse quadratic scaling with $\Delta t$ right there in the formula.

Yes I see, it makes sense, I'm still at the point of getting used to the symbols and positioning like when to multiply when no sign is shown or the symbol for pi being quite like a zero , I'm going to try and learn a bit of something new each day and everyday practice what I learnt the day before. It's always been my dream to learn the algebra, calculus, physics , math, I've always been a tinkerer and so often I wish I could have just calculated things out more in depth. Please feel free to continue teaching me anything you believe I need to know, thanks again

 

[pete94857]

@pete94857 I’d like to add to what @jbriggs444 has said,. You might want to try this…

A car has mass 1000kg (not ‘weight 1000kg’ by the way, because in physics 'weight' is a gravitational force measured in newtons!).

The car accelerates uniformly from rest and covers a distance of 100m in 10s.

a) What is the car’s initial speed?
b) What is the car’s average speed?
c) What is the car’s final speed?
d) What is the car’s final kinetic energy?

Your original problem isn’t that different from the above if you think about it. You are just using angles rather than distances and moment of inertia rather than mass.

A) The cars initial speed is zero as it is starting from rest.

The cars average speed 1 mile divided in 100 m is 1609.344 metres / 100 = 16.09344

16.09344 x 10 sec = 160.9344 sec per mile speed = 22.3693629 mile per hour
= 10 metres per second

Final speed of 20 metres per second.

KE = m x v = 1000 kg x 20 m/s = 200, 000 joules.

Can you please explain further a non uniformed acceleration

 

[Steve4Physics]

A) The cars initial speed is zero as it is starting from rest.

Yes

The cars average speed 1 mile divided in 100 m is 1609.344 metres / 100 = 16.09344

16.09344 x 10 sec = 160.9344 sec per mile speed = 22.3693629 mile per hour
= 10 metres per second

Not sure what happened!

You are told that the car covers a distance of 100 metres in 10 seconds. So average speed $= \frac {total~distance}{total~time} = \frac {100m}{10s} = 10m/s$.

Simple as that! No need to even think about miles and hours!

Final speed of 20 metres per second.

Yes.

KE = m x v = 1000 kg x 20 m/s = 200, 000 joules.

No. The correct formula for the kinetic energy of an object of mass $m$ moving at speed $v$ is KE $= \frac 12 mv^2$.

And 1000 x 20 is not 200,000.

Can you please explain further a non uniformed acceleration

Not sure what you are asking but see if this helps.

For uniform acceleration, speed changes at a steady rate, e.g. increases by 3m/s each second:
At t = 0, speed = 0
At t = 1s, speed = 3m/s
At t = 2s, speed = 6m/s
At t = 3s, speed = 9m/s

For non-uniform acceleration, speed doesn't change at a steady-rate, e.g.
At t = 0, speed = 0
At t = 1s, speed = 2m/s
At t = 2s, speed = 6m/s
At t = 3s. speed = 7m/s

Sometimes, calculations with non-uniform acceleration use calculus.

 

[pete94857]

Yes


Not sure what happened!

You are told that the car covers a distance of 100 metres in 10 seconds. So average speed $= \frac {total~distance}{total~time} = \frac {100m}{10s} = 10m/s$.

Simple as that! No need to even think about miles and hours!


Yes.


No. The correct formula for the kinetic energy of an object of mass $m$ moving at speed $v$ is KE $= \frac 12 mv^2$.

And 1000 x 20 is not 200,000.


Not sure what you are asking but see if this helps.

For uniform acceleration, speed changes at a steady rate, e.g. increases by 3m/s each second:
At t = 0, speed = 0
At t = 1s, speed = 3m/s
At t = 2s, speed = 6m/s
At t = 3s, speed = 9m/s

For non-uniform acceleration, speed doesn't change at a steady-rate, e.g.
At t = 0, speed = 0
At t = 1s, speed = 2m/s
At t = 2s, speed = 6m/s
At t = 3s. speed = 7m/s

Sometimes, calculations with non-uniform acceleration use calculus.

OK thanks... I converted to mph just for my own visualisation

 

[pete94857]

Yes


Not sure what happened!

You are told that the car covers a distance of 100 metres in 10 seconds. So average speed $= \frac {total~distance}{total~time} = \frac {100m}{10s} = 10m/s$.

Simple as that! No need to even think about miles and hours!


Yes.


No. The correct formula for the kinetic energy of an object of mass $m$ moving at speed $v$ is KE $= \frac 12 mv^2$.

And 1000 x 20 is not 200,000.


Not sure what you are asking but see if this helps.

For uniform acceleration, speed changes at a steady rate, e.g. increases by 3m/s each second:
At t = 0, speed = 0
At t = 1s, speed = 3m/s
At t = 2s, speed = 6m/s
At t = 3s, speed = 9m/s

For non-uniform acceleration, speed doesn't change at a steady-rate, e.g.
At t = 0, speed = 0
At t = 1s, speed = 2m/s
At t = 2s, speed = 6m/s
At t = 3s. speed = 7m/s

Sometimes, calculations with non-uniform acceleration use calculus.

Yes I do yet it I just had a very bad migraine yesterday but didn't want to be ignorant to your efforts I do really appreciate it thank you

 

[Steve4Physics]

Yes I do yet it I just had a very bad migraine yesterday but didn't want to be ignorant to your efforts I do really appreciate it thank you

No problem. Thank you. I hope the migraine is better. Keep well hydrated and avoid alcohol and caffeine!

Your final answer for the kinetic energy (200,00J) is correct. But it's important to realise (which you probably already do) that what you actually wrote:

KE = m x v = 1000 kg x 20 m/s = 200, 000 joules.

is wrong.

More importantly, you should see the correspondence between the orginal rotating cube problem and the accelerating car problem, They are both solved in the same way.

 

[pete94857]

I do thank you, I should have put KE = 1/2 ×I x Wf

 

[jbriggs444]

I do thank you, I should have put KE = 1/2 ×I x Wf

The correct formula is $KE = \frac{1}{2} \times I \times {\omega_f}^2$

Note that the $\omega_f$ is squared.

If you do not apply the factor of $\frac{1}{2}$ and do not square $\omega_f$ then the result will be angular momentum. We use the symbol "L" for angular momentum: $L = I \times \omega_f$.


In the car problem, the same applies. The correct formula is $KE = \frac{1}{2} \times m \times v^2$

If you do not apply the factor of $\frac{1}{2}$ and do not square $v$ then the result will be momentum. We use the symbol "p" for momentum: $p = m \times v$

 

[pete94857]

The correct formula is $KE = \frac{1}{2} \times I \times {\omega_f}^2$

Note that the $\omega_f$ is squared.

If you do not apply the factor of $\frac{1}{2}$ and do not square $\omega_f$ then the result will be angular momentum. We use the symbol "L" for angular momentum: $L = I \times \omega_f$.


In the car problem, the same applies. The correct formula is $KE = \frac{1}{2} \times m \times v^2$

If you do not apply the factor of $\frac{1}{2}$ and do not square $v$ then the result will be momentum. We use the symbol "p" for momentum: $p = m \times v$

Notes taken thank you