Kenneth Mann
- 424
- 3
30. Synchronous Circuit Example - - - 1 T0 12 Counter
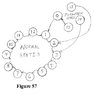
Now, we look at a counter which one person wanted to develop a couple of months back. This counter will count up to and include the value "12", but will not include the "0" value. If we want to know where such a counter would be used, we need only look at the standard "hour clock". It starts at the "One Oclock" value, and counts up to and past the "Twelve Oclock" value (though though the values from :"Twelve" to "One" are actually handled as the "Zero" values).
This counter is designed in a way much like that of the BCD counter. Again, four flip-flops are used, and we simply determine where these are to be toggled. Using the truth table the same way as before, it is filled out as is shown in figure 54. (Again, the lowest-order flip-flop simply toggles every time, and as such, is a trivial case and is not included in the truth-table. For each of the other flip-flops, and for the "carry out", we mark the place in the table (before) where the associated flip-flop is to be toggled.
This gives us the 'functions' (Jb, Jc, Jd and Co) which will go to the respective flip-flop J and K inputs, and enable them for toggling at the proper times.
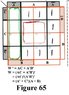
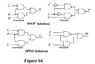
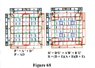
The table values are entered directly into their respectivr Karnaugh Maps, and solved. The maps are shown in figure 55. The logic diagram will be included in the next insertion.
KM
30. Synchronous Circuit Example - - - 1 T0 12 Counter
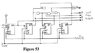
First, we note that figure 53 is of the BCD counter developed in the last insertion, but which we did not have space to show there.Now, we look at a counter which one person wanted to develop a couple of months back. This counter will count up to and include the value "12", but will not include the "0" value. If we want to know where such a counter would be used, we need only look at the standard "hour clock". It starts at the "One Oclock" value, and counts up to and past the "Twelve Oclock" value (though though the values from :"Twelve" to "One" are actually handled as the "Zero" values).
This counter is designed in a way much like that of the BCD counter. Again, four flip-flops are used, and we simply determine where these are to be toggled. Using the truth table the same way as before, it is filled out as is shown in figure 54. (Again, the lowest-order flip-flop simply toggles every time, and as such, is a trivial case and is not included in the truth-table. For each of the other flip-flops, and for the "carry out", we mark the place in the table (before) where the associated flip-flop is to be toggled.
This gives us the 'functions' (Jb, Jc, Jd and Co) which will go to the respective flip-flop J and K inputs, and enable them for toggling at the proper times.
The table values are entered directly into their respectivr Karnaugh Maps, and solved. The maps are shown in figure 55. The logic diagram will be included in the next insertion.
KM