Kelvin Units: Help Understand Optics of Graphene

[sukharef]

Hey!
In https://www.researchgate.net/publication/230937856_Optical_properties_of_graphene article (Optical properties of graphene) I found out the frequency is expressed in Kelvins.

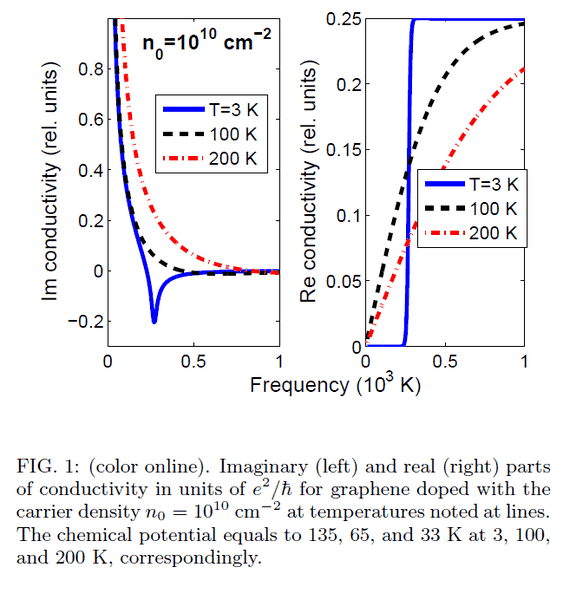
Could you help me with it - how did the author do this unit transformation?
Thanks in advance!

 

[John Park]

There are lots of units of "energy" that look like something else; frequency is a common one. In this case I think the author used E = k_bT, where k_b is the Boltzmann constant, together with E = hv, then equated the two formulae and dropped the k_b and the h. It works in such situations because both frequency and temperature are proportional to energy; and it's convenient to express quantities in terms of things you directly measure.

 

[sukharef]

There are lots of units of "energy" that look like something else; frequency is a common one. In this case I think the author used E = k_bT, where k_b is the Boltzmann constant, together with E = hv, then equated the two formulae and dropped the k_b and the h. It works in such situations because both frequency and temperature are proportional to energy; and it's convenient to express quantities in terms of things you directly measure.

Thank you for the answer!
What do you mean by dropping the k_b and the h? I mean, we can not just drop them without paying attention to the units that they are expressed in.
What should I do to turn the K-frequency into the sec--frequency in this situation? Still a little bit confused.

 

[DrClaude]

What is reported as "frequency" is actually $\hbar \omega / k_\mathrm{B}$.

 

[John Park]

What do you mean by dropping the kb and the h? I mean, we can not just drop them without paying attention to the units that they are expressed in.

Reference https://www.physicsforums.com/threads/frequency-in-k.907539/#post-5722451

Actually you can. As DrClaude says the frequency corresponds to ℏ ω / k.

Maybe think of it this way. We have an energy E that could be the energy of a photon with frequency ν, where hν = E. So we could just agree to talk about the frequency, knowing that if necessary we could always convert back to energies by multiplying by h. In the same way we could say that E =k_bT, using the Boltzmann constant to define a corresponding temperature T; and as long as we're talking about the same system we can compare energies, add or subtract them, by comparing, adding or subtracting the corresponding temperatures. We can always convert to real energies at any point, but there's usually no need.

Representing frequencies as temperatures just takes the same process one step further. It's a bit like expressing an amount in dollars as pounds sterling and as euros; you could use the results to express euros in terms of sterling.

 

[sukharef]

Actually you can. As DrClaude says the frequency corresponds to ℏ ω / k.

Maybe think of it this way. We have an energy E that could be the energy of a photon with frequency ν, where hν = E. So we could just agree to talk about the frequency, knowing that if necessary we could always convert back to energies by multiplying by h. In the same way we could say that E =k_bT, using the Boltzmann constant to define a corresponding temperature T; and as long as we're talking about the same system we can compare energies, add or subtract them, by comparing, adding or subtracting the corresponding temperatures. We can always convert to real energies at any point, but there's usually no need.

Representing frequencies as temperatures just takes the same process one step further. It's a bit like expressing an amount in dollars as pounds sterling and as euros; you could use the results to express euros in terms of sterling.

What is reported as "frequency" is actually $\hbar \omega / k_\mathrm{B}$.

Thank you!