- #1
jolindbe
- 12
- 0
Hi,
I have a bunch of spectra which happen to show some sinusoidal baselines, like this:
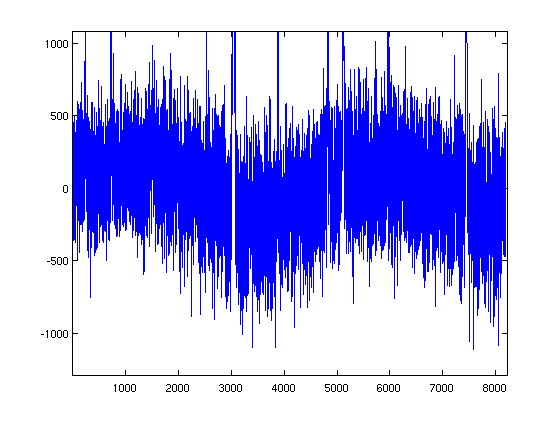
I would like to subtract these baselines somehow. Of course I can try to fit sinusoidals using for instance Matlab's lsqcurvefit, but it seems like I have to be very careful with my input guesses not to get completely insane results, which makes it very tedious for my spectra.
So I thought that I could do something about it in Fourier space instead. Just to try it out, I first made some dummy data (sinusoidal with similar frequency as in real data + Gaussian noise, no spectral lines), to see what that looks like in Fourier space:
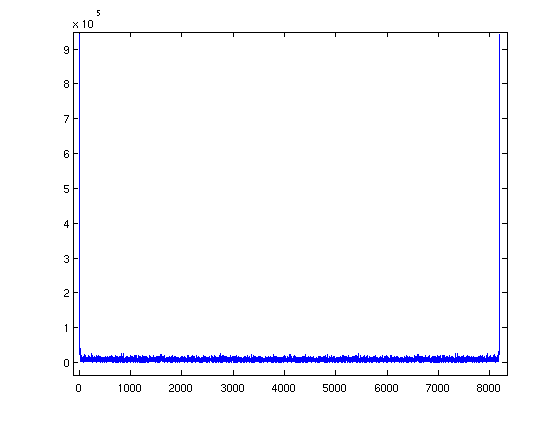
As you can see above, abs(fftdata) shows two very prominent spikes just on the edges of the spectrum, which sounds reasonable. The Fourier transform of a sine wave would be two dirac-deltas, and they should appear far out when the frequency is low compared to the spectral window. Let's try to kill it:
So above I have extracted the really high-amplitude parts of the Fourier spectrum, and subtracted them from the fft of the data, and taken the inverse fft of this. The result is fairly similar to wanted_data, and if I plot the difference of these I get this:
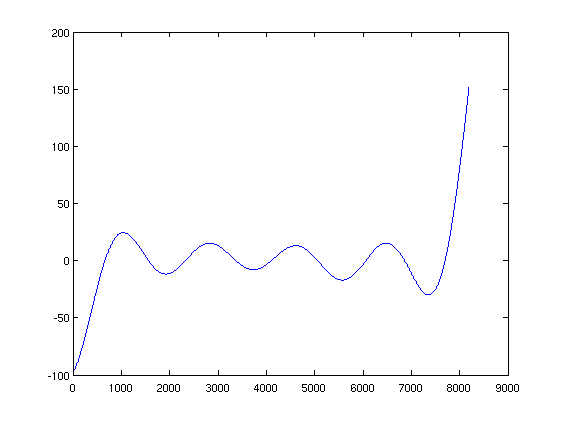
A new (higher-frequency) sine wave, but with a much lower amplitude than the original (by a factor of 10). Ok, it's not perfect, but this might actually work...
Let's make a try on the real data. The absolute value of the fft of the data looks like this:
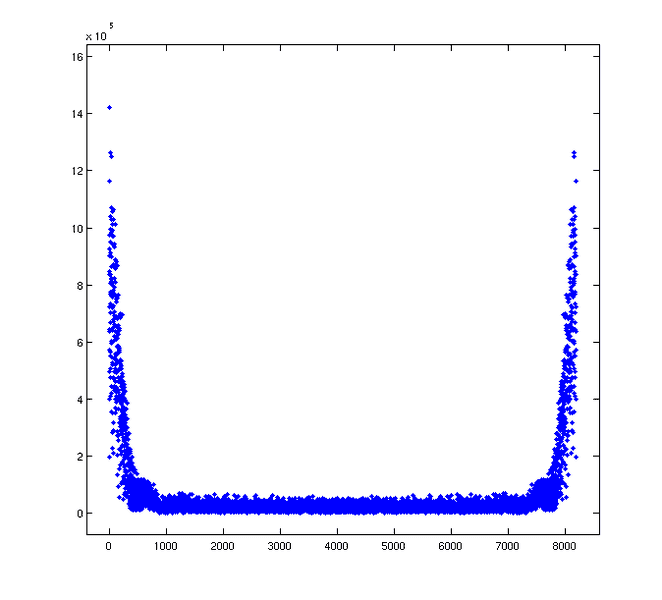
The features on the sides are much wider. How do I get rid of this? I have tried two methods:
Method 1: Subtracting all data with abs(fftdata) higher than a certain value (as above):
Method 2: Fitting polynomials to the outer edges, subtracting data scaled with this polynomial:
I can modify highval in Method 1, and nlim and degree in Method 2. But fiddling with the parameters does not produce great results, it seems like I either get very little result on my baseline, or that my signal-to-noise decreases a lot. Sometimes I get a different sinusoidal in my baseline instead (with much higher frequency).
Does anybody have a clue on how to treat that kind of data in the Fourier domain, or is the best way of solving it simply to give in and fit sinusoidals?
EDIT: My code above is in Matlab, but I also speak Python/numpy/scipy...
I have a bunch of spectra which happen to show some sinusoidal baselines, like this:
I would like to subtract these baselines somehow. Of course I can try to fit sinusoidals using for instance Matlab's lsqcurvefit, but it seems like I have to be very careful with my input guesses not to get completely insane results, which makes it very tedious for my spectra.
So I thought that I could do something about it in Fourier space instead. Just to try it out, I first made some dummy data (sinusoidal with similar frequency as in real data + Gaussian noise, no spectral lines), to see what that looks like in Fourier space:
Code:
N=8192;
t=1:N;
sinf = 250*sin(0.00135*t);
wanted_data = random('Normal',0,100,1,N);
data = sinf+wanted_data;
fftdata = fft(data)As you can see above, abs(fftdata) shows two very prominent spikes just on the edges of the spectrum, which sounds reasonable. The Fourier transform of a sine wave would be two dirac-deltas, and they should appear far out when the frequency is low compared to the spectral window. Let's try to kill it:
Code:
fft_approx = zeros(1,N);
fftdata = fft(data);
for i = 1:N
if abs(fftdata(i)) < 1e5
fft_approx(i) = 0;
else
fft_approx(i) = fftdata(i);
end
end
result_data = ifft(fftdata-fft_approx);So above I have extracted the really high-amplitude parts of the Fourier spectrum, and subtracted them from the fft of the data, and taken the inverse fft of this. The result is fairly similar to wanted_data, and if I plot the difference of these I get this:
A new (higher-frequency) sine wave, but with a much lower amplitude than the original (by a factor of 10). Ok, it's not perfect, but this might actually work...
Let's make a try on the real data. The absolute value of the fft of the data looks like this:
The features on the sides are much wider. How do I get rid of this? I have tried two methods:
Method 1: Subtracting all data with abs(fftdata) higher than a certain value (as above):
Code:
fft_approx = zeros(1,N);
fftdata = fft(data);
highval = 2e5;
for i = 1:N
if abs(fftdata(i)) < highval
fft_approx(i) = 0;
else
fft_approx(i) = fftdata(i);
end
end
result_data = ifft(fftdata-fft_approx);Method 2: Fitting polynomials to the outer edges, subtracting data scaled with this polynomial:
Code:
fft_pol = zeros(1,N);
fftdata = fft(data);
nlim = 500;
degree = 3;
p1 = polyfit(t(1:nlim),abs(fftdata(1:nlim)),degree);
p2 = polyfit(t(N-nlim:N),abs(fftdata(N-nlim:N)),degree);
for k = 1:N
if k <= nlim
fft_pol(k) = 1*polyval(p1,k)*fftdata(k)/abs(fftdata(k));
else
if k >= N-nlim+1
fft_pol(k) = 1*polyval(p1,N-k+1)*fftdata(k)/abs(fftdata(k));
else
fft_pol(k) = 0;
end
end
end
result_data = ifft(fftdata-fft_pol);I can modify highval in Method 1, and nlim and degree in Method 2. But fiddling with the parameters does not produce great results, it seems like I either get very little result on my baseline, or that my signal-to-noise decreases a lot. Sometimes I get a different sinusoidal in my baseline instead (with much higher frequency).
Does anybody have a clue on how to treat that kind of data in the Fourier domain, or is the best way of solving it simply to give in and fit sinusoidals?
EDIT: My code above is in Matlab, but I also speak Python/numpy/scipy...
Last edited:
) I was assuming that it was a power spectrum and the Y scale was some sort of logarithmic scale (hence the + and - signs), which is what you would normally present a spectrum(?). I, hence, was assuming that, in the absence of signal and with low noise, there would be a straight fuzzy base line somewhere along the lower half of the plot. The bumps would suggest that the noise is somehow modulated during the frequency sweep.