Satvik Pandey
- 591
- 12
Homework Statement
A mouse starts running on a circular path of Radius = 28m with constant speed u = 4m/s. A cat starts from the center of the path to catch the mouse. The cat always remains on the radius connecting the center of the circle and the mouse and it maintains magnitude of its velocity a constant v = 4m/s. How long (in sec) is the chase?
Homework Equations
ω=d\theta/dt
The Attempt at a Solution
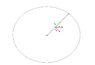
Before solving this problem I tried make a figure of this question.Here it is.
Hint given in my book says that in this problem angular velocities of cat and mouse are equal.
I know that angular velocity is change in angular displacement upon time.I am not sure about my figure.Please tell me if it is right or wrong and the angular velocity of cat and mouse are equal.It would be nice if you explain it with a figure.
[