Pruddy
- 64
- 0
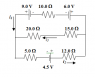
1) Please take a look at the attachment below in order to solve the problem. Using the figure at the right determine the values of i1, i2 and i3. Input your answers in the form "a.bc x 10^(y) A".2) Using the correct results from #1, determine the following. For A and B you must also tell if the current directions shown are correct. Give your answer in the requested format.
A. The current in the 10.0 resistor. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
B. The current in the 4.5 V battery. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
C. The voltage across the 15.0 resistor. Answer format: "ab.c V".
D. How much power is dissipated in the 5.0 resistor? Answer Format: "abc mW"
Loop: i1(10Ω) - 9.0V + 6.0 V - i3(15Ω+20Ω) = 0
Loop: i3(15Ω+20Ω)-i2(5Ω+12Ω) - 4.5V = 0
Loop: i1(10Ω) - 9.0V + 6.0V + i2(12Ω + 5Ω) - 4.5V = 0
Junction: i1 + i3 = i2
Please I would like to verify if my loop equations are correct and also to know how i can solve for i1, i2, and i3. Thanks a lot!
A. The current in the 10.0 resistor. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
B. The current in the 4.5 V battery. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
C. The voltage across the 15.0 resistor. Answer format: "ab.c V".
D. How much power is dissipated in the 5.0 resistor? Answer Format: "abc mW"
The Attempt at a Solution
Loop: i1(10Ω) - 9.0V + 6.0 V - i3(15Ω+20Ω) = 0
Loop: i3(15Ω+20Ω)-i2(5Ω+12Ω) - 4.5V = 0
Loop: i1(10Ω) - 9.0V + 6.0V + i2(12Ω + 5Ω) - 4.5V = 0
Junction: i1 + i3 = i2
Please I would like to verify if my loop equations are correct and also to know how i can solve for i1, i2, and i3. Thanks a lot!