- #1
room_
- 11
- 0
- TL;DR Summary
- I find the transfer function of the band-pass filter and its inverse Laplace yields not an impulse response but transient one.
I consider the band-pass filter of the following configuration (the ##u_m## is a voltage controlled voltage source):
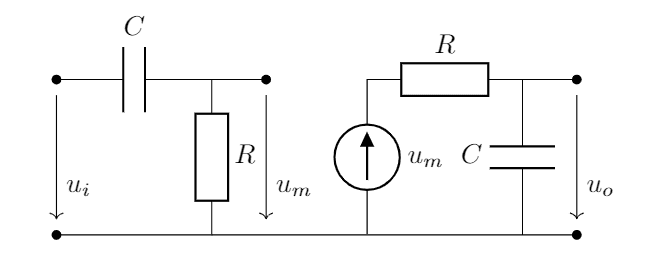The transfer function is
$$K_1(p)=\hat{U}_o(p) = \frac{p}{RC(p+1/RC)^2} = \frac{\omega_c p}{(p+\omega_c)^2}, \quad \omega_c=\frac{1}{RC}.\qquad (1)$$
Now I connect ##n## such filters in a row (using the ##u_o## of a previous one as a source for next's ##u_i## by means of the controlled voltage source), which means that the transfer function becomes
$$ K_n(p)=\frac{\omega_c^{n}p^{n}}{(p+\omega_c)^{2n}}. \qquad (2)$$
To compensate the decrease in voltage on cutoff (same as center here) frequency ##\omega_c## I add ##2^n## factor (since every filter decreases voltage twice):
$$ K_n(p)=\frac{2^n\omega_c^{n}p^{n}}{(p+\omega_c)^{2n}}.\qquad (3)$$
In some operational calculus handbook (russian one, not sure if it's reasonable to link) I find
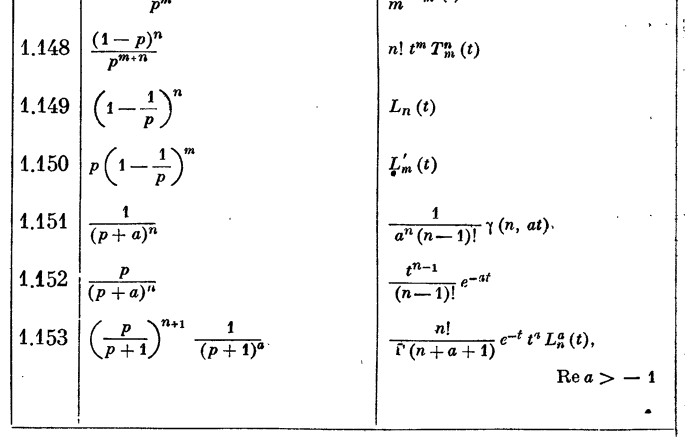I assume there is no problem in substituting ##n## for ##2n## in ##1.152##:
$$\hat{S}(p)=\frac{p}{(p+a)^{2n}}\div \frac{t^{2n-1}}{(2n-1)!}e^{-at}=s(t). \qquad(4) $$
Note that all of the derivatives of ##s(t)## up to ##n-2## order are equal to zero at ##t=0##. Finally I get the impulse response (using previous statement)
$$p^{n-1}2^n \omega_c^n \frac{p}{(p+\omega_c)^{2n}}-\sum_{k=0}^{n-2}p^{n-2-k} s^{(k)}(0) \div \frac{d^{n-1}}{dt^{n-1}} s(t),\qquad (5) \\
K_n(p)= \frac{2^n \omega_c^np^n}{(p+\omega_c)^{2n}}\div \frac{2^n\omega_c^n}{(2n-1)!}\frac{d^{n-1}}{dt^{n-1}}(e^{-\omega_c t}t^{2n-1})=k_n(t).\qquad (6)$$
I don't know why, but ##(6)## yields transient response (if to leave out the ##2^n## factor) ##h_n(t)## for my filter. i.e.
$$h_n(t)=\frac{\omega_c^n}{(2n-1)!}\frac{d^{n-1}}{dt^{n-1}}(e^{-\omega_c t}t^{2n-1}), \qquad (7)$$
although it is known that ##k(t)=\dfrac{d}{dt}h(t)##.
It is clear at least for ##n=1##. I plotted it in Matlab for ##n<30## (because Matlab refuses to calculate derivative of a higher order) and it looks
the way the simulation in NI Multisim gives. Here's ##n=49## (in Multisim):
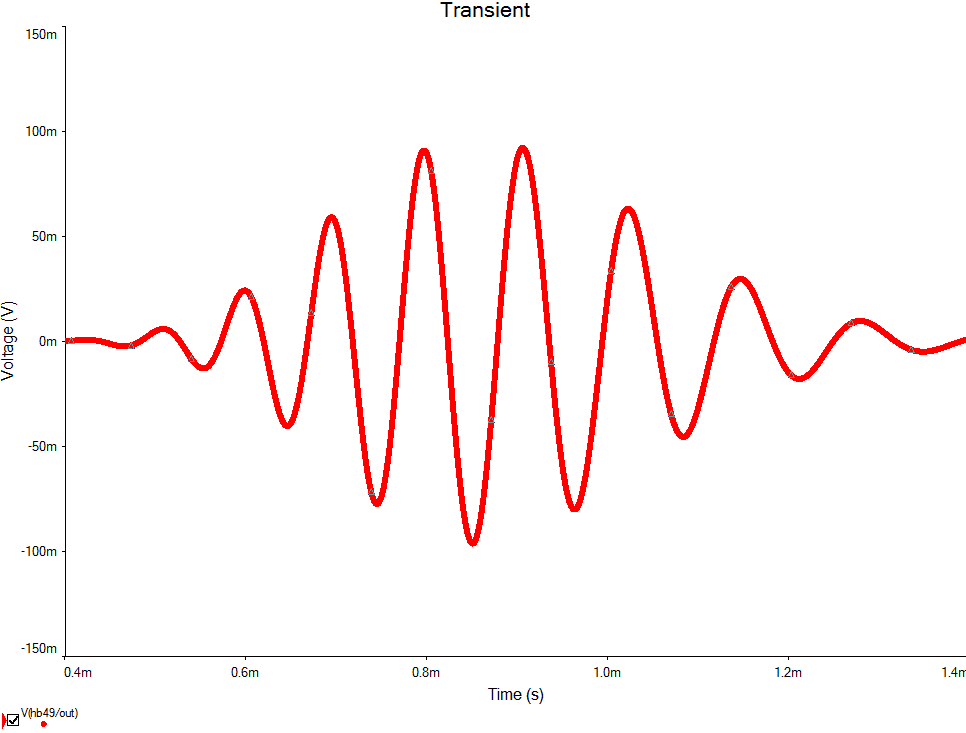It's predecessors (smaller ##n##'s) look alike, just having "less waves". WolframAlpha inverse Laplace suggestion (check my previous post) for transient response works for ##n\approx30\div50##, which is not satisfying. I assume there's something wrong with my reasoning, so I ask you to help me to find the mistake. Been struggling with it for a while and I need a fresh look on the problem. Thank you in advance.
$$K_1(p)=\hat{U}_o(p) = \frac{p}{RC(p+1/RC)^2} = \frac{\omega_c p}{(p+\omega_c)^2}, \quad \omega_c=\frac{1}{RC}.\qquad (1)$$
Now I connect ##n## such filters in a row (using the ##u_o## of a previous one as a source for next's ##u_i## by means of the controlled voltage source), which means that the transfer function becomes
$$ K_n(p)=\frac{\omega_c^{n}p^{n}}{(p+\omega_c)^{2n}}. \qquad (2)$$
To compensate the decrease in voltage on cutoff (same as center here) frequency ##\omega_c## I add ##2^n## factor (since every filter decreases voltage twice):
$$ K_n(p)=\frac{2^n\omega_c^{n}p^{n}}{(p+\omega_c)^{2n}}.\qquad (3)$$
In some operational calculus handbook (russian one, not sure if it's reasonable to link) I find
$$\hat{S}(p)=\frac{p}{(p+a)^{2n}}\div \frac{t^{2n-1}}{(2n-1)!}e^{-at}=s(t). \qquad(4) $$
Note that all of the derivatives of ##s(t)## up to ##n-2## order are equal to zero at ##t=0##. Finally I get the impulse response (using previous statement)
$$p^{n-1}2^n \omega_c^n \frac{p}{(p+\omega_c)^{2n}}-\sum_{k=0}^{n-2}p^{n-2-k} s^{(k)}(0) \div \frac{d^{n-1}}{dt^{n-1}} s(t),\qquad (5) \\
K_n(p)= \frac{2^n \omega_c^np^n}{(p+\omega_c)^{2n}}\div \frac{2^n\omega_c^n}{(2n-1)!}\frac{d^{n-1}}{dt^{n-1}}(e^{-\omega_c t}t^{2n-1})=k_n(t).\qquad (6)$$
I don't know why, but ##(6)## yields transient response (if to leave out the ##2^n## factor) ##h_n(t)## for my filter. i.e.
$$h_n(t)=\frac{\omega_c^n}{(2n-1)!}\frac{d^{n-1}}{dt^{n-1}}(e^{-\omega_c t}t^{2n-1}), \qquad (7)$$
although it is known that ##k(t)=\dfrac{d}{dt}h(t)##.
It is clear at least for ##n=1##. I plotted it in Matlab for ##n<30## (because Matlab refuses to calculate derivative of a higher order) and it looks
the way the simulation in NI Multisim gives. Here's ##n=49## (in Multisim):
)
